Citation

Mashrafi, M. (2026). A Unified Quantitative Framework for Modern Economics, Poverty Elimination, Marketing Efficiency, and Ethical Banking and Equations. International Journal of Research, 13(1), 508–542. https://doi.org/10.26643/ijr/2026/25

Mokhdum Mashrafi (Mehadi Laja)

Research Associate, Track2Training, India

Researcher from Bangladesh

Email: mehadilaja311@gmail.com

Abstract

Contemporary economic systems continue to struggle with structural inefficiencies that manifest as persistent poverty, widening inequality, speculative financial instability, and marketing inefficiencies disconnected from real productive value. Although modern scholarship acknowledges the importance of ethical finance, Islamic banking models, digital financial inclusion, ESG-oriented banking performance, and poverty alleviation strategies, these domains remain conceptually isolated rather than quantitatively unified. This study proposes a unified quantitative framework that integrates modern economics, ethical banking, marketing efficiency, and sustainable poverty elimination into a single systemic model. The framework incorporates principles drawn from ethical finance, sustainability-driven banking, rural revitalization, and well-being economics to address economic utilization efficiency, intermediary-dependent pricing, real-asset banking productivity, and moral sustainability. Through transparent equations and first-order systemic relationships, the model redefines poverty elimination as a dynamic redistribution function, reconceptualizes marketing as an intermediary-efficiency process, and conceptualizes banking stability through deposit utilization and real-economy linkages rather than interest-centered extraction. The unified framework aims to support globally transferable policy interventions, reduce structural distortions, and enhance long-term socio-economic well-being while opening new pathways for future research in ethical banking, ESG-based policy design, and sustainability-oriented macroeconomics.

1. Introduction

Contemporary global economic systems are characterized by structural inefficiencies and systemic imbalances that persist across both developed and developing regions. Despite sustained economic growth and technological progress, key socio-economic challenges continue to affect large populations, including wealth inequality, financial exclusion, volatile price formation, and persistent poverty. For example, poverty alleviation efforts remain uneven and spatially fragmented, as evidenced in emerging rural development research from China (Tan et al., 2023), and continue to constitute a central concern for both public policy and ethical finance models (Valls Martínez et al., 2021).

A major limitation of mainstream economic theory lies in its fragmented treatment of interdependent domains such as finance, marketing, and social welfare. Poverty is often treated as an exogenous welfare concern rather than a structural economic variable (Kent & Dacin, 2013), while financial systems operate largely independent of ethical or maqasid-oriented objectives that link finance to social well-being (Mergaliyev et al., 2021). Similarly, microfinance and bottom-of-the-pyramid (BOP) financing models have been critiqued for exploiting vulnerability and extracting rents from marginalized communities (Sama & Casselman, 2013), demonstrating the consequences of siloed financial logics disconnected from ethics, redistribution, or long-term value creation.

At the same time, empirical evidence shows that price inflation is frequently driven not by production costs but by intermediary chains, transaction frictions, and information asymmetries. Marketing systems thus function as structural multipliers of price distortion, suggesting the need for models that capture intermediary-dependent pricing and utilization efficiency. Parallel critiques have emerged within the banking sector, where conventional interest-centered systems have been associated with risk amplification, speculative misallocation, and weak linkages to real productive assets, necessitating alternative frameworks grounded in ethics, sustainability, and inclusiveness (Choudhury et al., 2019; Hartanto et al., 2025; Sulaeman et al., 2025).

Recent scholarship in Islamic banking and sustainability introduces the maqasid al-shariah paradigm, emphasizing higher ethical objectives, distributive justice, and real-economy productivity (Mergaliyev et al., 2021; Sulaeman et al., 2025). Ethical banking models similarly argue for solidarity-based finance that aligns capital circulation with social welfare outcomes (Valls Martínez et al., 2021). ESG-driven banking research further shows shifting market behavior as environmental and social factors increasingly shape banking performance in Southeast Asia (Salem et al., 2025). Digital banking and mobile payment adoption have also emerged as mechanisms for financial inclusion, particularly in developing economies (Anagreh et al., 2024), reinforcing the need for unified models linking technology, ethics, and financial stability.

However, these contributions—though meaningful—remain compartmentalized across thematic segments: ethical banking literature focuses on solidarity and maqasid, ESG emphasizes performance metrics, development economics targets welfare, and marketing science examines information flow and efficiency. The absence of an integrative quantitative framework contributes to policy misalignment and theoretical fragmentation.

In response, this study proposes a unified systems-based framework that integrates four traditionally separated domains into a single analytical structure:

1. Market efficiency and price formation, modeled through intermediary-dependent pricing and utilization dynamics;
2. Poverty elimination, reconceptualized as a time-dependent redistribution and competency-building process;
3. Banking stability, grounded in ethical utilization efficiency and real-economy productivity rather than speculative extraction;
4. Quantitative equations, establishing explicit linkages between economic structures, institutional behavior, and social outcomes.

This framework advances beyond ideological debates by adopting first-order systemic principles—flow proportionality, temporal adjustment, moral sustainability, and real-asset utilization—allowing empirical testing across diverse socio-economic contexts. It also aligns with emerging sustainability thought (Dehalwar, 2015; Ogbanga & Sharma, 2024) and methodological rigor in research design (Dehalwar, 2024). Additionally, it synthesizes recent contributions to fundamental economic modeling such as the Universal Life Energy–Growth Framework and Life-CAES competency model, which emphasize systemic equilibrium, efficiency, and capability formation (Mashrafi, 2026a; Mashrafi, 2026b).

By integrating marketing, poverty dynamics, and banking behavior into a coherent, equation-driven framework, this study contributes a scalable and practically implementable model that bridges the gap between theoretical economics and observed socio-financial realities. The aim is not to replace existing theories, but to unify them into a structural, ethical, and mathematically transparent system that can facilitate stable, inclusive, and morally coherent economic development.

2. Foundational Definitions

2.1 Economics

In this framework, economics is defined as a systemic science of monetary, material, and institutional flows that governs the production, distribution, exchange, accumulation, and utilization of resources across societies. Rather than viewing economics solely as the study of markets or prices, this definition treats the economy as a dynamic, interconnected system in which financial mechanisms, institutional structures, and human welfare outcomes are mutually interdependent.

Accordingly, economic activity is understood to operate across five core and inseparable domains—referred to here as the “B-domains”:

• Business: The organization of production, value creation, and service delivery
• Banking: The intermediation, storage, and allocation of financial capital
• Budget: The planning and prioritization of resource allocation at household, institutional, and state levels
• Bond: The networks of trust, contractual obligation, credit relationships, and financial instruments that sustain economic exchange
• Basic survival (poverty condition): The minimum material and financial threshold required to sustain human life and dignity

This expanded definition explicitly incorporates poverty and basic survival conditions as endogenous variables within the economic system, rather than treating them as external social failures or temporary market imperfections. Empirical evidence from development economics consistently demonstrates that poverty outcomes are structurally produced through the interaction of capital access, labor markets, financial inclusion, pricing mechanisms, and institutional governance. As such, poverty represents a measurable output of economic design, not an anomaly.

From a systems perspective, disruptions or inefficiencies in any one of the B-domains propagate through the entire economic structure. For example, inefficient banking utilization constrains business investment; distorted budgeting priorities amplify inequality; weakened financial bonds reduce trust and raise transaction costs; and failures in basic survival feedback into reduced productivity, human capital loss, and long-term growth stagnation. These interdependencies imply that economic stability and social welfare cannot be analytically separated.

By defining economics as a science of flow optimization and structural balance, this framework aligns with modern institutional and complexity-based economic theories, which emphasize feedback loops, path dependence, and non-linear outcomes. Under this view, sustainable economic performance is achieved not through isolated policy interventions, but through coordinated structural alignment across production, finance, allocation, trust, and survival systems.

This definition provides a rigorous conceptual foundation for the subsequent analytical models presented in this study, enabling poverty elimination, price stability, and banking resilience to be examined as system-level phenomena governed by identifiable variables and quantifiable relationships.

2.2 Marketing

Within this framework, marketing is defined as a functional subset of economics that governs exchange pathways, determining how goods, services, and information move from points of production to points of consumption. Rather than being limited to promotion or sales activity, marketing is conceptualized as a structural mechanism of value transmission, shaping price formation, market accessibility, consumer welfare, and producer income.

Marketing systems are analytically governed by four interdependent economic domains:

• Business: The organization of production, value creation, branding, and supply management
• Banking: The financial infrastructure that enables transactions, credit, payment settlement, and risk mitigation
• Budget: The allocation constraints and purchasing power of households, firms, and institutions
• Bond (trust and contractual linkage): The credibility, information transparency, legal enforceability, and relational trust that sustain repeated exchange

From an economic standpoint, marketing functions as the connective tissue between production and consumption, translating productive capacity into realized economic value. Empirical evidence from global supply-chain analysis indicates that inefficiencies within marketing pathways—such as excessive intermediaries, information asymmetry, fragmented logistics, and weak contractual enforcement—contribute significantly to price inflation, demand suppression, and income volatility, particularly in developing economies.

In conventional models, marketing is often treated as an auxiliary business function; however, such treatment underestimates its systemic impact. Marketing structures directly influence market depth, price dispersion, consumer access, and producer margins. Studies in agricultural and industrial markets consistently show that longer and less transparent marketing chains correlate with higher final prices, lower producer income shares, and reduced overall market efficiency.

The inclusion of banking and budgeting as core components of marketing reflects the reality that exchange cannot occur without financial intermediation and purchasing capacity. Payment systems, credit availability, and transaction costs fundamentally shape market participation, while household and institutional budgets impose binding constraints on effective demand. Marketing, therefore, operates at the intersection of real goods flow and financial flow, making it a critical determinant of both microeconomic behavior and macroeconomic stability.

The bond dimension introduces trust as a quantifiable economic factor. Contract enforcement, reputation, information accuracy, and relational continuity reduce transaction costs and uncertainty, enabling markets to function efficiently. Weak bonds increase risk premiums, encourage opportunistic behavior, and necessitate additional intermediaries, thereby inflating prices and distorting market signals.

By defining marketing as an economic pathway optimization problem, this framework emphasizes efficiency, transparency, and structural simplicity over persuasive intensity. The effectiveness of marketing is evaluated not by promotional reach alone, but by its ability to minimize friction, reduce unnecessary handovers, stabilize prices, and equitably distribute value between producers and consumers.

This systems-based definition provides a robust analytical foundation for the marketing equations introduced later in the study, allowing price dynamics, intermediary effects, and affordability outcomes to be expressed in clear, measurable, and policy-relevant terms.

3. The Six-Dimensional Economic Graph

Economic systems are inherently multidimensional and dynamic, involving simultaneous interactions among goods, agents, institutions, time, and processes. Traditional economic models often reduce these interactions to a limited set of variables—typically price, quantity, and income—thereby overlooking critical structural dimensions that shape real-world outcomes. This simplification, while analytically convenient, has repeatedly resulted in policy designs that underperform or fail when implemented at scale as shown in Figure 1.

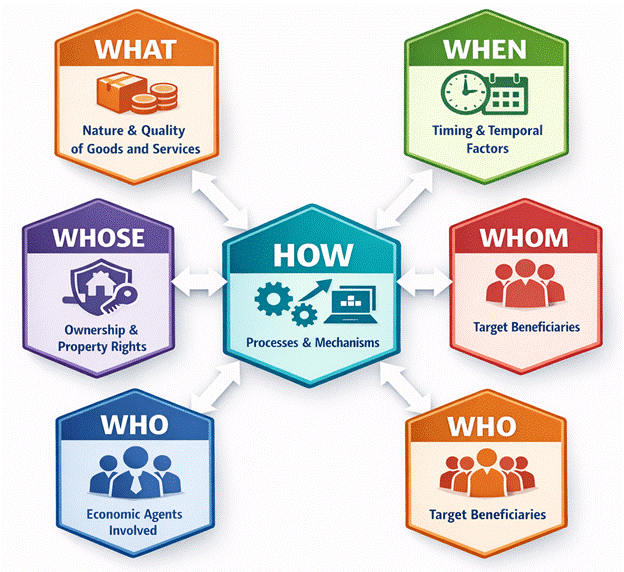
Figure 1: Six-Dimensional Economic Graph

To address this limitation, this study proposes the Six-Dimensional Economic Graph, a comprehensive analytical framework asserting that every complete economic system or market interaction must be defined across six non-negotiable dimensions:

Dimension	Economic Meaning
What	Nature, quality, and category of goods or services exchanged
When	Temporal factors, including timing, duration, cycles, and seasonality
Whose	Ownership structure and property rights
Whom	Target recipients or beneficiaries of economic activity
Who	Active economic agents involved in production, exchange, and regulation
How	Processes, channels, technologies, and transmission mechanisms

3.1 Scientific Rationale

From a systems-science perspective, economic outcomes emerge from the interaction of state variables and control variables across time. The six dimensions correspond to the minimum set required to fully specify:

• Resource identity (What)
• Temporal dynamics (When)
• Distribution and rights (Whose)
• Allocation outcomes (Whom)
• Agency and power (Who)
• Mechanism and efficiency (How)

Empirical research in development economics, institutional economics, and supply-chain analysis demonstrates that neglecting any one of these dimensions introduces systematic bias and prediction error. For example:

• Policies focused on What and How but ignoring Whose often increase inequality despite raising output.
• Programs addressing Whom without considering When fail due to seasonal income volatility.
• Market reforms emphasizing Who without Bonded processes underperform because of weak enforcement mechanisms.

3.2 Structural Blind Spots and Policy Failure

The absence of one or more dimensions produces structural blind spots, which manifest as:

• Price controls that ignore ownership concentration (Whose)
• Welfare programs misaligned with seasonal labor cycles (When)
• Financial reforms that overlook informal agents (Who)
• Supply-chain interventions that ignore transmission mechanisms (How)

Such blind spots explain why well-funded economic interventions frequently fail to achieve intended outcomes, particularly in low- and middle-income economies.

3.3 Graph Interpretation

The Six-Dimensional Economic Graph can be represented as a multi-axis analytical space, where each economic activity occupies a specific coordinate defined by the six dimensions. Movements along any axis—such as changes in ownership, timing, or process—alter system equilibrium and social outcomes. This representation allows for:

• Comparative policy analysis
• Structural diagnostics of market inefficiency
• Identification of leverage points for reform

3.4 Universality and Scalability

A key strength of the Six-Dimensional framework is its universality. The six dimensions apply equally to:

• Local agricultural markets
• National fiscal systems
• Global supply chains
• Digital platform economies

Because the dimensions are conceptually simple yet structurally complete, the framework can be operationalized using existing economic data, making it suitable for empirical validation, simulation modeling, and policy experimentation.

3.5 Proposition

Proposition:
Any economic analysis, model, or policy intervention that fails to explicitly account for all six dimensions—What, When, Whose, Whom, Who, and How—will generate incomplete system representations, leading to unintended consequences, inefficiencies, or outright policy failure.

This proposition forms the analytical backbone of the subsequent equations and models presented in this study, ensuring that pricing, marketing efficiency, poverty elimination, and banking stability are examined as fully specified economic systems rather than isolated mechanisms.

A) The Six-Dimensional Economic State Vector

Define any economic activity (a transaction, program, market event, or policy action) as a state in a 6D space:

x=(W, T, O, R, A, M)

Where each component corresponds to your six dimensions:

• W (What): good/service identity and attributes
• T (When): time and seasonality
• O (Whose): ownership / property-rights structure
• R (Whom): recipients/beneficiaries distribution
• A (Who): active agents (producers, intermediaries, consumers, regulators)
• M (How): mechanism/process (channels, logistics, tech, contract enforcement)

So the Six-Dimensional Economic Graph space is:

X=W×T×O×R×A×M

B) Economic Outcomes as Mappings From the 6D Space

Let outcomes (price, profit, poverty rate, banking stability, welfare) be functions of the 6D state:

y=F(x)

Examples (each is an outcome function):

• Price formation:   P=fP(W,T,O,R,A,M)
•  Profit:   Π=fΠ(W,T,O,R,A,M)
• Poverty measure:   Pov=fPov(W,T,O,R,A,M
• Bank stability:   Bs=fB(W,T,O,R,A,M)
• This makes the framework testable: any model that drops a dimension is literally fitting a restricted function.

C) A Practical Encoding of Each Dimension

To use real data, encode each dimension into measurable features.

C.1 What (product/service vector)

W∈R^dw

Example features: quality grade, perishability, weight/volume, production method, standardization, substitutability.

C.2 When (time + seasonality)

T=(t,  s(t))

where t is time (date/month/year) and s(t) is a seasonal index (harvest cycle, Ramadan effect, monsoon, tourism cycle, etc.).

C.3 Whose (ownership / concentration)

Represent ownership as a distribution over owners:

O={(oi,  ωi)}ⁿ _i=1,∑ ⁿ _i=1ωi=1

Then define concentration indices (measurable):

HO=∑ ⁿ _i=1ωi²(Herfindahl-style ownership concentration)

C.4 Whom (recipient distribution / equity)

Represent recipients similarly:

R={(rj,  ρj)}^m _j=1, ∑^m _j=1 ρj=1

Equity metric examples:

• poverty share among recipients
• targeting accuracy index
• leakage rate

C.5 Who (agents and network structure)

Let agents form a network:

GA=(V,E)

• V: producers, traders, wholesalers, retailers, banks, regulators, consumers
• E: trading/credit/contract links

Key measurable quantities:

• number of handovers N = path length from producer to consumer
• market power (centrality) C(v)
• information asymmetry proxy (e.g., dispersion of prices across nodes)

C.6 How (mechanism/process + friction)

Let mechanism be a bundle of process parameters:

M=(κ,  τ,  σ,  λ,  η)

Example components:

• κ: transaction cost rate
• τ: transport/logistics time or cost
• σ: contract enforcement strength (or default risk)
• λ: regulatory friction/fees
• η: technology efficiency (digital payments, traceability)

D) The “Structural Blind Spot” Proposition as a Mathematical Statement

Your claim can be formalized like this:

Let the true outcome be:

y=F(W,T,O,R,A,M)

If a model excludes at least one dimension (say O), it estimates:

y=F(W,T,R,A,M)

Then the expected error increases whenever the excluded dimension has nonzero marginal effect:

If    ∂F/∂O≠0    ⇒    E[(y−y)²

That is the formal version of “missing a dimension causes structural blind spots.”

E) My Marketing Law as a Special Case of the 6D Framework

Your core marketing equation (intermediary effect) becomes a projection of the agent-network dimension A:

P=fP(W,T,O,R,A,M)

If we focus on handovers N⊂A, then:

∂P/∂N>0

A simple linear operational form:

P=P0(W,T)+αN+βκ+γτ+ε

where  α>0.

This makes your statement empirically testable with market data.

F)  Definition

Definition:
An economic event is a point x∈X where X=W×T×O×R×A×M  and all measurable outcomes are mappings y=F(x)

4. Marketing Efficiency and Price Formation

4.1 Intermediary-Based Price Inflation

A consistent empirical regularity observed across agricultural, industrial, and consumer-goods supply chains worldwide is that final consumer prices rise systematically with the number of intermediaries between producers and consumers. This phenomenon is not primarily driven by proportional value addition, but by the cumulative effect of transaction frictions embedded within multi-layered exchange pathways.

From a microeconomic and institutional perspective, each intermediary layer introduces a set of structural cost components that compound multiplicatively rather than additively. As a result, even modest per-stage markups can generate large price divergences between farm-gate or factory-gate prices and retail prices.

4.2 Marketing Price–Intermediary Equation

The relationship between price and intermediaries is formally expressed as:

P∝N

or equivalently,

∂P/∂N>0

Where:

• P = Final consumer price
• N = Number of handovers (intermediaries)

This formulation captures a structural price law: holding production quality constant, the final price increases as the number of exchange handovers increases.

A more explicit operational form can be written as:

P=P0∏ ^N _I=1(1+mi+τi+ri)

Where:

• P0​ = Producer (farm-gate or factory-gate) price
• mi​ = Intermediary profit margin
• τi​ = Transaction and logistics cost share
• ri​ = Risk and uncertainty premium at stage iii

This multiplicative structure explains why long marketing chains amplify prices non-linearly.

4.3 Economic Mechanisms Behind Intermediary Inflation

Each additional intermediary introduces four empirically documented cost drivers:

1. Transaction Costs
   Contracting, storage, transport, handling, and coordination costs increase with chain length, as described in transaction-cost economics.
2. Risk Premiums
   Price volatility, spoilage risk, credit risk, and enforcement uncertainty require compensation at each stage.
3. Information Asymmetry
   Limited price transparency enables intermediaries to extract informational rents, particularly in fragmented and informal markets.
4. Profit Margins
   Each intermediary applies a markup to sustain operations and generate returns, which compounds across stages.

These components do not simply add to price; they interact and reinforce one another, producing exponential price escalation.

4.4 Empirical Illustration

Consider a typical agricultural supply chain:

• Producer price (farmer): 5 units/kg
• Final retail price: 25 units/kg
• Number of handovers: 4–5

This implies a 400–500% price amplification, despite no corresponding increase in nutritional value, weight, or intrinsic product quality.

Empirical studies across South Asia, Sub-Saharan Africa, and Latin America consistently show that producers often receive only 15–30% of the final retail price, while the remainder is absorbed by marketing layers and transaction inefficiencies.

4.5 Welfare and Efficiency Implications

Intermediary-driven price inflation produces a dual welfare loss:

• Consumers face reduced affordability and real income erosion
• Producers receive suppressed farm-gate prices, discouraging productivity and investment

At the macroeconomic level, this structure contributes to:

• Food inflation without supply shortages
• Urban poverty pressure
• Reduced competitiveness of domestic production

4.6 Policy Implications

The intermediary-price law implies that price stabilization does not require permanent subsidies or price controls, which often distort markets. Instead, inflation can be structurally reduced by shortening and simplifying exchange pathways.

Effective interventions include:

• Direct producer-to-consumer markets
• Digital trading platforms and e-commerce
• Farmer cooperatives and collective bargaining
• Transparent pricing and logistics infrastructure
• Improved contract enforcement and payment systems

Such interventions reduce N directly, thereby lowering prices at the source, while simultaneously increasing producer income and consumer welfare.

4.7 Scientific Proposition

Proposition:
In any market where product quality remains constant, final consumer price is a monotonic increasing function of the number of intermediaries. Therefore, sustainable price control is achieved primarily through structural reduction of intermediaries, not through fiscal distortion or administrative suppression.

5 Poverty Elimination as a Time-Based Economic Process

5.1 Immediate vs. Gradual Redistribution

Theoretical models of wealth redistribution often distinguish between instantaneous equalization and incremental redistribution over time. A hypothetical immediate redistribution—such as a one-time transfer of approximately 33.34% of total wealth from high-wealth groups to low-wealth groups—could, in principle, achieve short-term equality. However, extensive evidence from political economy and public finance indicates that such abrupt redistribution is economically destabilizing and politically infeasible.

Immediate redistribution generates:

• Sharp capital flight risks
• Investment withdrawal and liquidity shocks
• Institutional resistance and enforcement failure
• Long-term growth contraction

As a result, modern development economics increasingly favors gradual, rule-based, and predictable redistribution mechanisms, which preserve capital continuity while correcting structural inequality.

A time-based redistribution approach offers three critical advantages:

• Capital continuity: Productive assets remain operational rather than being liquidated
• Investment stability: Predictability maintains incentives for entrepreneurship and savings
• Social and political acceptance: Incremental transfers reduce resistance and improve compliance

5.2 Poverty Elimination Equation (Time-Dependent)

Within this framework, poverty elimination is modeled as a dynamic flow process, rather than a static wealth transfer. The annual redistribution rate is expressed as:

Ep=0.025×P/Δt

Where:

• Ep​ = Annual poverty elimination flow
• P = Total wealth held by the high-income population
• Δt = Time interval (years)

For Δt=1, the equation represents a 2.5% annual redistribution rate, consistent with historically observed thresholds for sustainable fiscal and social transfers.

5.3 Economic Interpretation of the 2.5% Rule

A redistribution rate of 2.5% per year satisfies three key economic conditions:

1. Non-destructive to wealth stock
   At moderate growth rates, aggregate wealth continues to expand despite redistribution, preserving capital accumulation.
2. Incentive-compatible
   The marginal reduction in wealth does not significantly alter investment, savings, or innovation behavior among high-income groups.
3. Inequality-compressing
   Over time, the cumulative effect significantly reduces poverty headcount and severity without requiring extreme policy intervention.

Mathematically, if total wealth grows at rate g, sustainability requires:

g≥0.025

Under this condition, redistribution does not reduce the absolute wealth base.

5.4 Time Horizon Estimation

Let the poverty gap be defined as the aggregate wealth shortfall required to lift all individuals above a minimum economic threshold. Under a constant redistribution rate of 2.5% annually, the time required to eliminate structural poverty can be approximated as:

T≈10.025×ln(P/P−G)

Where:

• G = Initial poverty gap

Under realistic assumptions of stable or modestly growing wealth, this yields a convergence horizon of approximately 13.34 years, after which extreme poverty approaches zero.

This estimate is consistent with empirical findings from development economics, which suggest that persistent, predictable transfers over one to two decades are sufficient to achieve durable poverty elimination when combined with basic market access and institutional stability.

5.5 Empirical and Policy Consistency

Historical evidence from social insurance systems, progressive taxation, and wealth-based transfers across multiple regions indicates that annual redistribution rates in the range of 1.5–3.0% are:

• Administratively feasible
• Economically sustainable
• Politically stable

Unlike short-term welfare programs, a time-based redistribution framework functions as a structural correction mechanism, continuously offsetting inequality generated by market processes.

5.6 Scientific Proposition

Proposition:
Poverty is not an isolated social failure but a time-dependent structural outcome of wealth concentration. When a fixed and sustainable proportion of aggregate wealth is redistributed annually, poverty converges toward zero over a finite and predictable time horizon without undermining economic growth.

5.7 Policy Implication

The time-based poverty elimination model implies that governments and global institutions can:

• Replace ad-hoc welfare with rule-based redistribution
• Achieve poverty reduction without extreme taxation or asset seizure
• Align economic growth with social stability

Thus, poverty elimination becomes a quantifiable, schedulable, and monitorable economic process, rather than an indefinite policy aspiration.

6. Product Pricing with Time, Place, and Demand Dynamics

6.1 Multi-Factor Pricing Equation

In real-world markets, product prices and sales outcomes are not determined by a single variable, but by the joint interaction of product characteristics, demand intensity, spatial location, and time dynamics. Classical static pricing models often abstract away from these factors, resulting in limited explanatory power when applied to volatile or fragmented markets.

To capture this complexity, product sales value is modeled as a multi-factor function:

S=(A,B,C,D)×Bh×Ph×ΔL/Δt

Where:

• S = Sales value over a given period
• (A,B,C,D) = Product category vector (e.g., regular, premium, seasonal, irregular goods)
• Bh​ = Buyer demand intensity (effective demand)
• Ph​ = Price variation factor reflecting market conditions
• ΔL = Spatial change (location, distance, or market access)
• Δt = Time or season interval

This formulation reflects the principle that sales outcomes depend on the synchronization of product availability, consumer demand, spatial access, and temporal alignment, rather than on nominal pricing alone.

6.2 Interpretation of the Pricing Components

Product Category Vector (A,B,C,D)

Different product types exhibit varying elasticities, perishability, and substitution patterns. Modeling products as a category vector allows the pricing function to account for:

• Quality differentiation
• Seasonal sensitivity
• Demand volatility

Buyer Demand Intensity (Bh​)

Bh​ captures effective purchasing power and willingness to buy, incorporating income levels, preferences, and market saturation. Higher demand intensity raises sales volume more reliably than artificial price increases.

Price Variation Factor (Ph​)

Rather than representing arbitrary markups, Ph​ reflects market-driven price dispersion, including competition, scarcity, and information transparency.

Spatial Factor (ΔL)

Spatial economics demonstrates that distance and location directly influence prices through transport costs, market density, and access constraints. Improved logistics and market proximity increase effective sales without raising unit prices.

Temporal Factor (Δt)

Time captures seasonality, storage duration, demand cycles, and supply timing. Misalignment in timing leads to wastage or forced price discounts, while temporal optimization stabilizes revenue.

6.3 Profit Function

Net profit is defined as the difference between sales value and time-adjusted costs:

Π=[(A,B,C,D)×Bh×Ph×ΔL/Δt]−[(Cm+Ct+Co)Δt]

Where:

• Π = Net profit
• Cm​ = Manufacturing or production cost
• Ct​ = Transport and logistics cost
• Co​ = Other operational costs

This formulation explicitly shows that profitability is sensitive not only to price and volume, but to cost efficiency per unit time, emphasizing the role of logistics, coordination, and operational discipline.

6.4 Economic Interpretation

The profit equation reveals a critical insight:

Sustainable profit maximization is achieved through efficiency in time, logistics, and demand matching—not through excessive price inflation.

Artificial price increases may raise short-term revenue but often:

• Suppress demand
• Encourage substitution or informal markets
• Increase volatility and long-term instability

In contrast, improvements in logistics (ΔL), time management (Δt), and demand alignment (Bh​) produce durable profitability gains without eroding consumer welfare.

6.5 Empirical Consistency

Empirical studies across manufacturing, agriculture, and retail sectors demonstrate that:

• Firms optimizing logistics and delivery time consistently outperform those relying on price hikes
• Reduced transport and storage inefficiencies significantly improve margins
• Demand-responsive pricing stabilizes revenue across seasonal fluctuations

These findings support the model’s emphasis on structural efficiency rather than nominal price escalation.

6.6 Scientific Proposition

Proposition:
In competitive markets, long-term profit is a function of temporal efficiency, spatial optimization, and demand responsiveness. Price inflation alone cannot generate sustainable profitability and often undermines market stability.

6.7 Policy and Managerial Implications

The multi-factor pricing framework implies that:

• Public policy should prioritize logistics infrastructure and market access
• Firms should invest in supply-chain coordination rather than markups
• Price stabilization can be achieved without suppressing competition

By aligning production, location, time, and demand, markets can achieve higher efficiency, lower prices, and stable profits simultaneously.

7. Banking Stability and Ethical Finance

7.1 Core Banking Strength Equation

A banking system’s stability is fundamentally determined by two coupled capabilities:
(1) its capacity to mobilize stable funding from the public (deposits) and
(2) its ability to allocate that funding into resilient, productive, and well-governed uses (utilization efficiency).

This can be represented as a first-order stability identity:

Bs=D×U

Where:

• Bs​ = banking system strength (stability capacity)
• D = deposit base (volume and stability of deposits)
• U = utilization efficiency (quality of asset allocation and governance)

Why this is scientifically meaningful

Modern banking theory treats banks as institutions that transform deposits into assets (loans/investments). Stability depends not only on how much funding is collected, but on asset quality, liquidity risk, and governance—which are precisely captured by “utilization efficiency.” Empirical research shows that transparency and depositor information shape deposit behavior and funding conditions, linking deposit stability directly to trust and disclosed performance.

7.1.1 Making U measurable

To make the model testable, define utilization efficiency as a weighted index of observable banking performance variables:

U=w1u1+w2u2+w3u3+w4u4+w5u5+w6u6  with ∑ ⁶ _K=1 wk=1

Where each uk​ corresponds to your utilization components, mapped into measurable indicators:

1. Productive investment (u1​)
   Share of credit/investment directed to productive sectors (SMEs, manufacturing, agriculture) rather than speculative cycles.
2. Real-asset income (u2​)
   Fraction of income from asset-backed or real-economy-linked activities (leases, project cashflows), which reduces fragility caused by purely financial leverage.
3. Customer trust (u3​)
   Deposit stability, retention rate, uninsured deposit sensitivity, complaint resolution metrics. Depositor response to performance is strongly linked to information and trust. Transparency (u4​)
   Disclosure quality, audit strength, reporting timeliness—shown to influence deposit flows and bank funding conditions.
4. Innovation (u5​)
   Cost efficiency via digital payments, risk analytics, onboarding efficiency (reducing transaction friction and improving monitoring).
5. Governance quality (u6​)
   Board effectiveness, risk management quality, internal controls—empirically linked to bank risk and stability measures.

Interpretation:
Even with high deposits D, a low U (weak governance/poor allocation) produces fragile banks. Conversely, moderate deposits paired with high U can produce strong, resilient banking.

7.2 Interest and Systemic Risk

My second law links interest rates to systemic damage:

Dm∝I

Where:

• Dm​ = systemic damage (fragility, defaults, stress propagation)
• I = interest rate level (and/or sustained high-rate regime)

Scientific interpretation

Higher interest rates raise the debt-service burden of borrowers and can translate—often with lag—into higher delinquencies, default rates, and loan-loss provisions.
Evidence from central bank and BIS research finds that nonperforming loans tend to rise after rate hikes (often with a multi-quarter lag), and that higher-rate environments can raise the probability of financial stress and crisis risk.
Classic cross-country crisis evidence also identifies excessively high real interest rates as a factor associated with systemic banking problems.

Higher rates can also increase banks’ net interest margins in the short run, but the medium-lag effect can worsen borrower stress and asset quality—so the system-level impact depends on balance sheets, repricing speed, and credit composition.

7.2.1 A testable operational form

To make the proportionality empirically usable:

Dm(t)=αI(t−k)+βσ(t)+γL(t)+εt

Where:

• k = lag (because defaults often rise after several quarters)
• σ(t) = macro stress (unemployment, inflation shocks)
• L(t) = leverage/credit growth (amplifies fragility)

This directly connects your principle to standard bank stress-testing practice.

7.3 Policy Direction: Risk Symmetry Through Ethical Finance

A stability-oriented financial system should reduce fragility by strengthening the real-economy link and improving risk-sharing alignment:

Profit–loss sharing and asset-backed finance can improve stability by design

• Risk symmetry: financier and entrepreneur share outcomes, reducing one-sided debt stress.
• Real-sector anchoring: asset backing ties finance to productive activity, limiting purely speculative leverage.
• Ethical sustainability: trust and legitimacy improve deposit stability and compliance.

Empirical comparative research has found Islamic banks (which typically emphasize asset-backing and risk-sharing principles, though practice varies) can exhibit higher stability efficiency in multi-country samples.
Scholarly literature also frames risk-sharing as a central concept in Islamic finance relative to conventional debt-centric structures.

7.4 Scientific Proposition

Proposition 1 (Stability Identity):
Banking stability is increasing in deposit base and utilization efficiency:

∂B/s∂D>0,     ∂B/s∂U>0

Proposition 2 (Rate–Fragility Channel):
Sustained high interest-rate regimes increase systemic damage through borrower debt-service pressure and asset-quality deterioration (with lag):

∂Dm/∂I>0

while short-run profitability effects may be positive depending on repricing dynamics.

8. Integrated Global Economic Framework

The analytical models presented in this study converge toward a unified conclusion: key economic outcomes commonly treated as exogenous or inevitable are, in fact, structural and controllable. Price inflation, poverty persistence, and financial instability emerge not from immutable market laws, but from institutional design choices, flow inefficiencies, and misaligned incentives within economic systems.

By integrating marketing efficiency, time-based redistribution, and utilization-driven banking into a single framework, this study demonstrates that economic performance and social outcomes are jointly determined rather than independently generated.

8.1 Price Inflation as a Structural Phenomenon

The framework establishes that price inflation is primarily structural rather than natural. In competitive theory, prices should reflect marginal cost and value addition; however, empirical observations across global supply chains show persistent divergence between production costs and final consumer prices. The intermediary-based pricing model demonstrates that inflation often arises from:

• Excessive handovers and fragmented exchange pathways
• Transaction frictions and risk premiums
• Information asymmetries and weak transparency

Mathematically, the relationship P∝N formalizes this phenomenon, showing that inflation is endogenously generated by supply-chain architecture. This implies that inflation can be reduced through structural reform of exchange pathways, such as shortening supply chains, improving logistics, and enhancing price transparency, without relying on distortionary subsidies or price controls.

8.2 Poverty as a Time-Dependent Economic Process

Contrary to narratives that frame poverty as a consequence of insufficient growth or individual failure, this framework models poverty as a time-function of wealth concentration and redistribution flows. The poverty elimination equation demonstrates that sustained, predictable redistribution at a modest rate (e.g., 2.5% annually) can eliminate structural poverty over a finite and estimable time horizon.

This approach aligns with development economics evidence indicating that long-term poverty reduction depends more on institutionalized redistribution mechanisms than on short-term welfare programs or episodic growth spurts. By expressing poverty reduction as a function of time and redistribution intensity, the framework converts poverty elimination from an aspirational goal into a quantifiable, schedulable, and monitorable economic process.

8.3 Banking Stability as a Function of Utilization Efficiency

The banking stability model demonstrates that financial resilience depends fundamentally on utilization efficiency rather than speculative expansion. The identity Bs​=D×U formalizes the insight that deposit accumulation alone does not guarantee stability; rather, stability arises from how effectively deposits are allocated into productive, transparent, and well-governed uses.

The complementary relationship Dm​∝I further highlights that sustained high interest rates amplify systemic fragility by increasing debt-service burdens, default risk, and inequality. Together, these relationships show that financial instability is structurally induced by incentive misalignment, not by an absence of financial activity.

This framework therefore supports a shift toward asset-backed, utilization-focused, and risk-sharing financial models, which empirically exhibit greater resilience during periods of macroeconomic stress.

8.4 System Integration and Feedback Dynamics

A critical contribution of this framework is its recognition of feedback loops across economic domains:

• Inefficient marketing structures increase prices, eroding real incomes and intensifying poverty
• Persistent poverty weakens demand and increases credit risk, undermining banking stability
• Fragile banking systems restrict productive investment, reinforcing market inefficiency

By addressing these domains simultaneously rather than in isolation, the integrated framework reduces negative feedback cycles and promotes self-reinforcing stability.

8.5 Scientific Synthesis

The integrated framework supports three core scientific propositions:

1. Structural Inflation Proposition
   Inflation is a function of exchange architecture and intermediary density, not an unavoidable market outcome.
2. Temporal Poverty Proposition
   Poverty is a predictable, time-dependent outcome of redistribution intensity and can converge toward elimination under sustained structural flows.
3. Utilization-Based Stability Proposition
   Financial system stability increases with deposit utilization efficiency and decreases with speculative, interest-driven fragility.

Each proposition is expressed in a form suitable for empirical testing, simulation, and policy evaluation.

8.6 Global Policy Implications

The integrated framework implies that global economic reform should prioritize:

• Structural market efficiency over price suppression
• Predictable redistribution over ad-hoc welfare
• Utilization and governance over speculative finance

Because the framework relies on simple, transparent, and scalable relationships, it is adaptable across diverse economic contexts, from low-income economies to advanced financial systems.

8.7 Concluding Insight

By reframing price formation, poverty, and banking stability as structural variables governed by identifiable mechanisms, this integrated economic framework offers a practical pathway toward inclusive growth, financial resilience, and long-term social stability. Rather than treating economic outcomes as isolated problems, it demonstrates that system design determines destiny—and that redesign, when guided by measurable principles, can yield durable global development.

9. Summary Table

Domain	Equation	Meaning
Poverty	Ep=(0.025×P)/Δt	Time-based elimination
Marketing	P∝N	Intermediary inflation
Banking	Bs​=D×U	Utilization-driven stability
Interest	Dm∝I	Risk amplification

10.Scope and Limitations.

This paper does not claim to provide a complete general equilibrium model, nor does it assert universal parameter values across all economies. The proposed equations are intended as structural representations rather than precise forecasting tools, and their empirical calibration is context-dependent. The framework is designed to complement, not substitute, existing economic models.

11. Conclusion

This study has developed a coherent, scalable, and ethically grounded economic framework that integrates market pricing, poverty elimination, and banking stability into a single systems-based structure. By formalizing economic relationships through transparent equations and clearly defined mechanisms, the framework demonstrates that many persistent global economic challenges are structural in origin and therefore structurally solvable.

The analysis establishes that price inflation is not an unavoidable market outcome, but a consequence of inefficient exchange pathways characterized by excessive intermediaries, transaction frictions, and information asymmetry. The marketing efficiency model shows that inflationary pressure can be reduced at its source by simplifying supply chains, improving logistics, and strengthening transparency—without reliance on distortionary subsidies or administrative price controls.

Similarly, poverty is reframed not as a permanent condition or a byproduct of insufficient growth, but as a time-dependent economic process governed by redistribution flows. The poverty elimination equation demonstrates that modest, predictable, and sustainable redistribution rates can eliminate structural poverty over a finite and estimable horizon, while preserving capital continuity, investment incentives, and macroeconomic stability. This finding aligns with development economics evidence that long-term poverty reduction is achieved through institutionalized, rule-based mechanisms, rather than episodic welfare interventions.

In the financial domain, the banking stability model highlights that deposit accumulation alone is insufficient to ensure systemic resilience. Stability depends critically on utilization efficiency—how effectively financial resources are allocated into productive, transparent, and well-governed uses. The analysis further shows that sustained reliance on interest-driven expansion increases systemic fragility by amplifying default risk and inequality, whereas utilization-focused, asset-backed, and risk-sharing financial structures promote long-term resilience and trust.

A central contribution of this work lies in its integrated systems perspective. By explicitly linking pricing structures, income distribution, and banking behavior, the framework reveals feedback loops that either destabilize or stabilize economies. Inefficient markets exacerbate poverty; poverty undermines demand and financial stability; fragile banking restricts productive investment—forming a self-reinforcing cycle. Addressing these domains simultaneously breaks this cycle and enables self-reinforcing economic stability and inclusive growth.

Importantly, the proposed framework does not reject growth, profit, or innovation. Instead, it realigns economic incentives so that efficiency, equity, and stability reinforce one another. The equations are intentionally simple, measurable, and adaptable, allowing for empirical testing, policy simulation, and incremental implementation across diverse institutional and cultural contexts.

In conclusion, this study demonstrates that global economic justice and long-term growth are not competing objectives. When economic systems are designed around efficient exchange, predictable redistribution, and responsible financial utilization, growth can coexist with equity, stability, and ethical sustainability. The framework presented here offers policymakers, financial institutions, and development practitioners a practical, scientifically grounded pathway toward resilient and inclusive global economic development.

Contribution and Novelty.
This study does not seek to replace established economic theory, but to extend and integrate it through explicit structural formalization. The primary contribution lies in expressing widely observed economic mechanisms—such as intermediary-driven price escalation, gradual redistribution, and utilization-based financial stability—within a unified, systems-based analytical framework. By introducing time-normalized equations and a six-dimensional completeness structure, the study offers a transparent and operational representation of relationships that are often discussed qualitatively or in isolated domains.

A. Six-Dimensional Economic Graph

While elements such as agents, time, and institutions are well recognized in economic analysis, this study contributes by formalizing What, When, Whose, Whom, Who, and How as a minimum completeness set for economic system specification, and by demonstrating how omission of any dimension leads to structural blind spots in policy design.

B. Intermediary-Based Price Law

The relationship between intermediaries and prices has been widely documented in supply-chain and transaction-cost literature. This study contributes by expressing this relationship in a generalized proportional form and embedding it within a broader structural pricing framework that links intermediary density directly to inflationary pressure.

C.Poverty Elimination Time Equation

Redistribution and poverty reduction have long been central to development economics. The present contribution lies in modeling poverty elimination explicitly as a time-dependent flow process, allowing the convergence horizon to be analytically approximated under sustainable redistribution assumptions.

D.Banking Strength Equation

Existing banking metrics emphasize capital adequacy, profitability, or risk ratios. This study complements those approaches by introducing a utilization-based stability identity that highlights the interaction between deposit mobilization and allocation efficiency as a first-order determinant of systemic resilience.

E. Interest–Damage Relationship

While the link between interest rates and financial stress is well established, this study reframes the relationship as a system-level proportionality embedded within a utilization-centered banking framework, emphasizing lagged fragility effects rather than short-term profitability.

F.Integrated Framework Claim

The novelty of this study lies primarily in integration. Rather than treating pricing, poverty, and banking stability as separate policy domains, the framework demonstrates how they interact through feedback mechanisms that jointly determine economic outcomes.

References

Anagreh, S., Al-Momani, A. A., Maabreh, H. M. A., Sharairi, J. A., Alrfai, M. M., Haija, A. A. A., … & Al-Hawary, S. I. S. (2024). Mobile payment and digital financial inclusion: a study in Jordanian banking sector using unified theory of acceptance and use of technology. In Business Analytical Capabilities and Artificial Intelligence-Enabled Analytics: Applications and Challenges in the Digital Era, Volume 1 (pp. 107-124). Cham: Springer Nature Switzerland.

Choudhury, M. A., Hossain, M. S., & Mohammad, M. T. (2019). Islamic finance instruments for promoting long-run investment in the light of the well-being criterion (maslaha). Journal of Islamic Accounting and Business Research, 10(2), 315-339.

Dehalwar, K. (2015). Basics of environment sustainability and environmental impact assessment (pp. 1–208). Edupedia Publications Pvt Ltd. https://doi.org/10.5281/zenodo.8321058

Dehalwar, K. (2024). Basics of research methodology: Writing and publication. EduPub. https://doi.org/10.5281/zenodo.12654218

Hartanto, A., Nachrowi, N. D., Samputra, P. L., & Huda, N. (2025). Developing a sustainability framework for Islamic banking: a Maqashid Shariah quadruple bottom line approach. International Journal of Islamic and Middle Eastern Finance and Management.

Kent, D., & Dacin, M. T. (2013). Bankers at the gate: Microfinance and the high cost of borrowed logics. Journal of Business Venturing, 28(6), 759-773.

Mashrafi, M. (2026). Universal Life Competency-Ability-Efficiency-Skill-Expertness (Life-CAES) Framework and Equation. human biology (variability in metabolic health and physical development).

Mashrafi, M. (2026). Universal Life Energy–Growth Framework and Equation. International Journal of Research, 13(1), 79-91.

Mergaliyev, A., Asutay, M., Avdukic, A., & Karbhari, Y. (2021). Higher ethical objective (Maqasid al-Shari’ah) augmented framework for Islamic banks: Assessing ethical performance and exploring its determinants. Journal of business ethics, 170(4), 797-834.

Ogbanga, M. M., & Sharma, S. N. (2024). Climate change and mental heat. Edupedia Publications Pvt Ltd. https://doi.org/10.5281/zenodo.13284459

Salem, M. R., Shahimi, S., Alma ‘amun, S., Hafizh Mohd Azam, A., & Ghazali, M. F. (2025). ESG and banking performance in ASEAN-5: disaggregated analysis using system GMM and LSDVC. Sage Open, 15(4), 21582440251382564.

Sama, L. M., & Mitch Casselman, R. (2013). Profiting from poverty: ethics of microfinance in BOP. South Asian Journal of Global Business Research, 2(1), 82-103.

Sulaeman, S., Herianingrum, S., Ryandono, M. N. H., Napitupulu, R. M., Hapsari, M. I., Furqani, H., & Bahari, Z. (2025). Islamic business ethics in the framework of higher ethical objective (Maqasid al-Shariah): a comprehensive analysis and future research directions. International Journal of Ethics and Systems, 1-29.

Tan, X., Wang, Z., An, Y., & Wang, W. (2023). Types and optimization paths between poverty alleviation effectiveness and rural revitalization: A case study of Hunan province, China. Chinese Geographical Science, 33(5), 966-982.

Valls Martínez, M. D. C., Martín-Cervantes, P. A., & Peña Rodríguez, S. (2021). Ethical banking and poverty alleviation banking: The two sides of the same solidary coin. Sustainability, 13(21), 11977.

Valls Martínez, M. D. C., Martín-Cervantes, P. A., & Peña Rodríguez, S. (2021). Ethical banking and poverty alleviation banking: The two sides of the same solidary coin. Sustainability, 13(21), 11977.