Domain-Dependent Validity of an Inequality Derived from a Classical Absolute Value Identity

Mashrafi, M. (2026). Domain-Dependent Validity of an Inequality Derived from a Classical Absolute Value Identity. International Journal for Social Studies, 12(1), 32–42. https://doi.org/10.26643/ijss/2026/2

Mokhdum Mashrafi (Mehadi Laja)
Research Associate, Track2Training, India
Researcher from Bangladesh
Email: mehadilaja311@gmail.com

Abstract

The classical identity √(−Y)² = |Y| is universally valid for all real Y, arising from the principal square root and absolute value definitions. However, when this identity is reformulated as an inequality—namely √(−Y)² ≤ Y—its validity becomes domain-restricted rather than universal. This paper provides a rigorous analytical examination of the inequality and demonstrates that it holds if and only if Y ≥ 0. For Y < 0 the inequality fails due to the non-negativity constraint imposed by the principal square root. The results highlight that transforming universally valid equalities into inequalities introduces implicit logical constraints not visible in the original formulation. The findings underscore the importance of explicit domain awareness in algebraic reasoning, inequality analysis, and pedagogical practice.

Keywords: absolute value, inequality analysis, real numbers, square root, domain restriction, algebraic logic

1. Introduction

In elementary algebra and real analysis, one encounters a variety of foundational identities that appear deceptively simple yet encode nontrivial conceptual structures. Among these, the identity involving the principal square root of a squared real number, expressed in the canonical form √Y² = |Y|, occupies a central role in the theory of real-valued functions. This identity asserts that for any real number Y, applying the squaring operation followed by the principal square root yields the absolute value of Y rather than its original signed value. This result follows directly from two fundamental conventions: first, that the square of a real quantity is always non-negative; and second, that the principal square root function √· is defined to produce the unique non-negative real number whose square equals the input. Together, these conventions enforce that √Y² is never negative, even when Y itself is negative, thereby establishing equality with |Y| rather than Y.

The identity plays a crucial role in various branches of mathematics, including algebraic manipulation, analytic proofs, metric theory, inequality systems, vector calculus, and optimization frameworks. Students typically learn to apply this identity when simplifying radical expressions, solving equations involving absolute values, or analyzing distance functions in Euclidean space. Despite its ubiquity, the pedagogical presentation of this identity is often terse, leaving little room for discussing conceptual subtleties such as the principal value convention, the distinction between signed and unsigned magnitudes, or the domain-sensitive implications of logical transformations involving equalities and inequalities.

A particularly underexplored aspect arises when one considers not merely the identity itself, but transformations that involve replacing the equality sign with inequality symbols. In mathematical analysis, it is common to convert identities into inequalities when considering bounding relationships, constraint satisfaction, feasibility regions, or optimization criteria. Such transformations appear simple at first glance, yet they may introduce implicit logical restrictions on variable domains that are not evident in the original identity. For example, one might ask whether the expression √Y² ≤ Y holds for all real Y, or equivalently whether |Y| ≤ Y is universally valid. While the original equality √Y² = |Y| holds for every real number, the transformed inequality does not: it is satisfied only for non-negative values of Y. For negative values of Y, the expression fails, because |Y| becomes strictly greater than Y, reflecting the fact that the absolute value function removes sign rather than preserving it.

This observation illustrates a deeper conceptual phenomenon in mathematics: equalities can be logically symmetric and universally valid across entire domains, whereas inequalities typically encode asymmetric relations that depend critically on the sign, order, or domain of the variable. When transforming an equality into an inequality, one may unintentionally impose additional constraints that were absent in the original formulation. In the case of √Y² = |Y|, the identity is unconditional, and no assumptions about the sign of Y are required. However, the inequality √Y² ≤ Y implicitly demands that Y be non-negative, since √Y² represents a non-negative quantity while Y may take negative values. Thus, the inequality is neither universally valid nor equivalent to the original identity, but instead defines a proper subset of the real number system—namely the set of all Y such that Y ≥ 0.

The distinction between these two statements underscores the importance of domain awareness in algebraic reasoning. In textbooks and classroom instruction, students are rarely encouraged to interrogate domain restrictions unless explicitly solving inequalities or piecewise-defined functions. However, understanding when and why domain restrictions emerge is critical not only for higher mathematics, but also for applied fields such as optimization, control theory, computational modeling, and machine learning, where constraints and feasibility sets determine the correctness of solutions.

From a logical and pedagogical standpoint, the inequality-based interpretation of √(−Y)² is especially intriguing. One might initially assume that since squaring removes sign information and the square root function returns a non-negative output, the expression √(−Y)² is algebraically interchangeable with √Y². Indeed, in terms of algebraic value, both reduce to |Y| without exception. Yet, when comparing √(−Y)² directly to Y rather than |Y|, the sign of Y becomes decisive. For Y ≥ 0, both √Y² and Y yield the same non-negative value, and the inequality √(−Y)² ≤ Y is satisfied as an equality. For Y < 0, however, the expression √(−Y)² equals −Y, which is strictly positive, while Y itself is negative; hence the inequality fails. This introduces a stark boundary at zero, revealing that what was once an unconditional equality can become a conditional statement partitioning the real line into validity and invalidity regions.

This study focuses precisely on these logical and domain-sensitive implications. By examining the expression √(−Y)² and its relational comparison with Y through the inequality √(−Y)² ≤ Y, the work aims to clarify how subtle domain conditions emerge from inequality reformulation. Although √(−Y)² equals |Y| algebraically, the inequality introduces a nontrivial domain constraint dependent on the sign of Y. Through formal characterization, this analysis demonstrates that such transformations are not merely symbolic exercises, but encode structural truths about real-number operations, sign behavior, and the semantics of comparison operators.

The broader significance lies in reinforcing a more rigorous culture of algebraic thinking. Mathematics is full of statements that appear obvious in one form yet reveal deeper layers when expressed differently. By making these layers explicit, we gain more refined tools for both teaching and research, encouraging learners to transition from procedural manipulation to conceptual understanding. The exploration presented here is therefore not merely a technical exercise, but an illustration of how foundational algebraic concepts can continue to yield insights when viewed through new interpretive lenses.

2. Methods

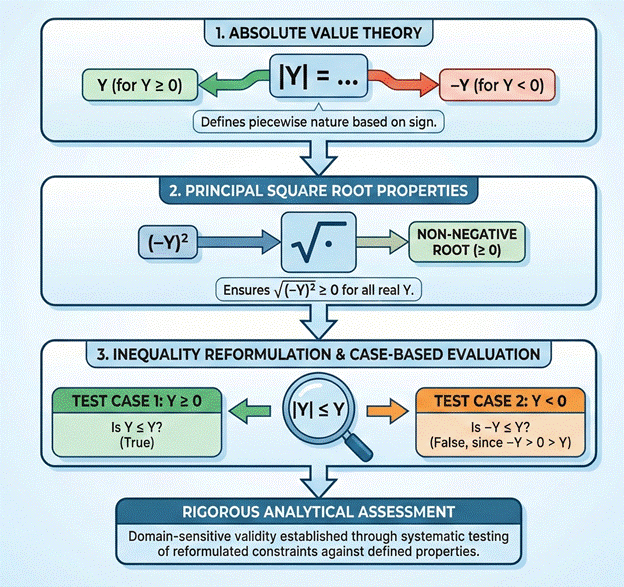
Figure 1: Analytical framework

The analytical framework employed in this study draws upon foundational concepts from real analysis, algebraic logic, and inequality theory. The objective of the methodological approach is to determine the domain-specific conditions under which the inequality holds, despite the universal validity of the underlying identity . The approach proceeds through three interconnected methodological components, each of which contributes to a rigorous evaluation of domain-sensitive validity.

1. Absolute Value Theory

The starting point of the analysis relies on the theoretical definition of the absolute value function. For any real number , the absolute value is defined piecewise as:

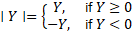
This definition encapsulates the notion that absolute value represents magnitude without sign. In the context of the present study, the expression reduces directly to , which provides a bridge between radical expressions and piecewise-defined functions. By introducing this piecewise structure, the method explicitly anticipates that different domain intervals (such as and ) will exhibit different behaviors with respect to the target inequality.

2. Principal Square Root Properties

The second methodological component involves formal properties of the principal square root operator , which is defined to yield the non-negative real number whose square equals the argument. This definition is essential because it ensures for all . In the current context, since squaring eliminates sign, the expression is always non-negative, and thus its principal square root satisfies for every real . This property plays a determinant role when comparing with , because if , the left-hand side becomes non-negative while the right-hand side becomes strictly negative, creating an inherent asymmetry.

3. Inequality Reformulation and Case-Based Evaluation

The final component reformulates the inequality analytically. Using the equality , the target inequality becomes . Since is piecewise-defined, the inequality must be evaluated separately for the intervals and . This case-based evaluation allows the study to determine precisely where the inequality holds and where it fails, yielding a domain-sensitive conclusion.

Together, these three methodological steps provide a structured and rigorous framework for analyzing domain-dependent validity in algebraic inequalities.

3. Results

3.1 Reformulation

From:

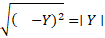
the inequality becomes:

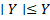
The first step in the analytical process involves rewriting the given radical expression in a form that reveals its algebraic structure more transparently. Starting from the expression , we note that it follows the same transformation principle as the more common form . In both cases, the squaring operation eliminates the sign information of the inner quantity, producing a non-negative result, and the principal square root operator returns the non-negative magnitude. This allows us to invoke the well-established identity for any real number . Accordingly, if we treat as the inner argument, its squared value will be non-negative, and therefore . When the specific expression simplifies to , the identity becomes , reflecting the magnitude of independently of its sign. This reformulation bridges radical expressions with absolute value theory and sets the stage for inequality-based reasoning.

Once the radical expression has been converted into absolute value notation, the inequality under study becomes significantly more tractable. The original inequality involving the square root can now be expressed in terms of absolute values as . This transformation is crucial for two reasons. First, it replaces a radical expression with a piecewise-defined function, which naturally leads to domain-based interpretation. Second, it makes explicit that the analytical challenge is no longer about evaluating a square root, but rather about understanding how the sign of influences the relationship between and . Since the absolute value function either preserves or negates its input depending on its sign, the reformulated inequality highlights that the validity of the original inequality hinges entirely on the sign of . The reformulation therefore serves as a critical methodological link between symbolic manipulation and domain-sensitive inequality analysis.

3.2 Domain Evaluation

Two cases are analyzed:

• Case 1: Y ≥ 0
  Here |Y| = Y, so the inequality holds as equality.
• Case 2: Y < 0
  Here |Y| = −Y > Y, so the inequality fails.

After reformulating the expression into the inequality , the next step is to determine the domain over which this inequality holds true. Since the absolute value function is defined in a piecewise manner, its behavior depends on the sign of . Therefore, the evaluation naturally requires a division of the real number line into distinct intervals corresponding to non-negative and negative values of . This case-based approach is essential because the inequality may demonstrate different logical outcomes in each interval, even though the original identity is universally valid over all real numbers.

In the first case, when , the definition of the absolute value function reduces to . Substituting this into the inequality yields , which holds as an equality. Consequently, for all non-negative values of , the original inequality is satisfied. In the second case, when , the definition of absolute value becomes . Since whenever is negative, the substituted inequality becomes , which is false. Thus, no negative value of satisfies the inequality. The case-based evaluation therefore reveals a sharp contrast between positive and negative domains, demonstrating that sign plays a decisive role in the inequality’s validity.

3.3 Final Result

The inequality holds if and only if:

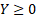
Based on the above domain evaluation, it becomes clear that the inequality — and by extension — is not universally valid over the real numbers. Instead, its validity is restricted to those values of for which the absolute value function does not introduce a sign change. Formally, the inequality holds if and only if . For all values of , the inequality fails because the non-negative output of the principal square root cannot be less than or equal to a negative input.

This result highlights a crucial conceptual conclusion: while algebraic equalities involving radicals and squares can be universally valid, inequalities derived from them may exhibit domain-dependent truth conditions. The sign of the variable becomes the determining factor, turning a seemingly simple expression into a conditional statement about subsets of the real line.

4. Discussion

The results show that converting a universally valid equality into an inequality introduces domain constraints not present in the original expression. The principal square root ensures a non-negative outcome, which creates sign-sensitive relational effects when compared with an unrestricted real variable.

The findings of this study demonstrate that transforming a universally valid algebraic equality into an inequality can fundamentally alter the logical conditions under which the resulting statement remains true. The identity is valid for all real values of because it rests on definitions that apply unconditionally over the real number system: squaring removes sign information, and the principal square root returns the non-negative magnitude of its argument. However, once the equality is reformulated into the inequality , the universal validity disappears. The inequality no longer holds for all ; instead, its validity becomes contingent on the sign of , yielding a domain restriction to . This shift from an unrestricted to a restricted domain illustrates how relational operators such as ≤ or ≥ introduce asymmetry into statements that were originally symmetric under equality.

A key reason for this shift lies in the non-negativity constraint embedded within the principal square root function. The operator is defined to return the unique non-negative real number whose square equals the input. As a result, is always non-negative, while itself may be negative. When the inequality compares a non-negative quantity to a potentially negative one, a sign conflict arises: if , then , making the inequality false. This asymmetry is invisible in the original equality because equality imposes a bidirectional condition of equivalence that is satisfied regardless of sign. In contrast, inequality imposes a directional relation that only holds over a restricted subset of values. The result reinforces the broader principle that inequality reasoning requires more careful attention to sign behavior and functional range than equality reasoning does.

More broadly, this analysis reveals an important conceptual insight: a universally true algebraic identity can become a conditionally true inequality depending on the relational operator and the assumed domain of discourse. This observation is frequently overlooked in routine algebraic instruction, where students learn to manipulate symbols in a procedural manner without explicitly considering domain constraints. For instance, many algebraic techniques—such as applying square roots, dividing by variables, or expanding absolute values—are valid only under certain domain assumptions. When these assumptions remain implicit, errors may arise in both computation and reasoning. The present study highlights the need to make such assumptions explicit, particularly in foundational learning environments.

This insight has practical implications beyond pure algebra. In real analysis, inequalities often act as tools for bounding functions, defining convergence criteria, or establishing continuity and differentiability properties. In optimization and constraint modeling, inequalities define feasible solution spaces, control stability conditions, and determine whether a candidate solution satisfies required constraints. In such contexts, misunderstanding domain restrictions can lead to incorrect feasible sets, invalid assumptions about optimality, or flawed proofs regarding solution existence. Awareness of domain conditions therefore contributes directly to mathematical rigor and theoretical correctness.

The pedagogical implications are equally significant. Modern mathematics education has increasingly emphasized conceptual understanding over mechanical symbol manipulation. Encouraging students to reflect on domain assumptions and the behavior of functions under relational transformation aligns with this goal. By presenting examples such as the inequality derived from , instructors can illustrate how expressions that seem trivial in equality form can become nontrivial when reinterpreted under inequalities. Such instruction fosters more robust logical reasoning and prepares students for advanced topics where domain issues are central, including measure theory, functional analysis, and numerical methods.

Finally, the discussion situates this work within the broader context of algebraic logic. Algebraic expressions are not merely computational artifacts but encode structural relationships governed by definitions, operators, and domains. Recognizing how these components interact is essential to understanding when and why mathematical statements hold. The present study contributes to this understanding by clarifying how the interplay between the principal square root, absolute value, and inequality operators generates domain-sensitive outcomes. Taken together, these observations reinforce that seemingly simple manipulations can have deep logical consequences, and that mathematical rigor requires attention not just to formulas, but to the structural assumptions they implicitly carry.

More broadly, this reveals that:

A universally true equality can yield a conditionally true inequality depending on the relational operator and domain assumptions.

This insight is relevant in real analysis, constraint modeling, and mathematical pedagogy, where rigor and domain awareness are crucial. Highlighting such constraints supports conceptual understanding and discourages overly procedural manipulation without logical interpretation.

5. Conclusion

The inequality derived from the classical identity holds only for non-negative values of Y. While the equality form is valid for all real numbers, the inequality form becomes domain-restricted. This demonstrates the importance of recognizing implicit logical constraints when performing algebraic transformations involving inequalities.

This study examined the inequality obtained from a classical algebraic identity and demonstrated that its validity is restricted to a subset of the real number system. While the underlying equality holds universally for all real values of , the derived inequality is satisfied only when . For , the inequality fails due to the non-negativity of the principal square root, which produces values that cannot be less than or equal to negative quantities. This contrast highlights a key conceptual point: equality-based identities may retain validity over entire domains, whereas their inequality counterparts may introduce implicit restrictions that alter the set of permissible input values.

The results emphasize the importance of recognizing and articulating domain assumptions when performing algebraic transformations, particularly those involving inequalities and absolute values. Failure to acknowledge such constraints can lead to incorrect conclusions, especially in contexts involving optimization, analysis, and proof-based reasoning. By making these logical boundaries explicit, this work contributes to a deeper understanding of how structural properties of functions shape mathematical statements, and it underscores the pedagogical value of treating equalities and inequalities not as interchangeable symbolic forms, but as distinct logical objects with different domain implications.

References

Mashrafi, M. (2026). Universal Life Energy–Growth Framework and Equation. International Journal of Research, 13(1), 79–91.

Mashrafi, M. (2026). Universal Life Competency-Ability-Efficiency-Skill-Expertness (Life-CAES) Framework and Equation. Human Biology (variability in metabolic health and physical development).

Lamberti, P. D., & de Cristoforis, M. L. (2005). A global Lipschitz continuity result for a domain-dependent Neumann eigenvalue problem for the Laplace operator. Journal of Differential Equations, 216(1), 109–133.

Finnie, G., & Sun, Z. (2002). Similarity and metrics in case‐based reasoning. International Journal of Intelligent Systems, 17(3), 273–287.

Harari, I., & Hughes, T. J. (1992). What are C and h?: Inequalities for the analysis and design of finite element methods. Computer Methods in Applied Mechanics and Engineering, 97(2), 157–192.

Segu, M., Tonioni, A., & Tombari, F. (2023). Batch normalization embeddings for deep domain generalization. Pattern Recognition, 135, 109115.

Huo, T., et al. (2025). A novel domain generalization network integrating invariance and cohesiveness for rolling bearing fault diagnosis. Structural Health Monitoring.

Vänskä, S., & Taskinen, M. (2008). Domain dependent Dirac’s delta and derivatives with an application to electromagnetic boundary integral representations. Journal of Mathematical Analysis and Applications, 344(1), 546–556.

Schatz, A. H. (1980). A weak discrete maximum principle and stability of the finite element method in . Mathematics of Computation, 34(149), 77–91.

Dun, A., Geng, Z., & Huang, L. (2011). Design of controller for Lur’e systems guaranteeing dichotomy. Applied Mathematics and Computation, 217(22), 8927–8935.

Long, M., Wang, J., Sun, J., & Yu, P. S. (2014). Domain invariant transfer kernel learning. IEEE Transactions on Knowledge and Data Engineering, 27(6), 1519–1532.

Tseng, V. S., Chen, L. C., & Kao, C. P. (2008). Constrained clustering for gene expression data mining. In PAKDD (pp. 759–766). Springer.