Mashrafi, M. (2026). Economics Equation: A Conceptual Framework and Mathematical Symbolic Model for Economic Development and Growth. Journal for Studies in Management and Planning, 12(1), 65–74. https://doi.org/10.26643/jsmap/2026/3

Mokhdum Mashrafi (Mehadi Laja)
Research Associate, Track2Training, India
Researcher from Bangladesh
Email: mehadilaja311@gmail.com

Abstract

This paper proposes a conceptual economic framework, titled Economics Equation–3, to explain how economies transition from low or medium development levels to stronger and sustainable growth trajectories. Drawing from economic systems theory, conceptual modeling, and symbolic mathematical reasoning, the model identifies and integrates key positive growth factors, market flow dynamics, and negative constraints into a unified symbolic structure. The framework considers the interaction between product characteristics, manpower, market accessibility, policy intervention, and temporal–spatial variation. The study aligns with existing literature emphasizing the role of conceptual frameworks in modern economics, mathematical modeling for growth, and evolutionary economic theory (Fusfeld, 1980; Debreu, 1984; Dopfer, 2005; Vasconcelos, 2013; Czerwinski, 2024). The resulting conceptual model is intended to support future empirical studies, economic policy analysis, business strategy formulation, and long-term development planning. The work remains theoretical and hypothesis-driven, highlighting the need for empirical validation in diverse economic contexts.

1. Introduction

Economic development has long been understood as a multidimensional and evolutionary process that extends beyond the influence of any single variable. Rather than emerging from isolated improvements in production, technology, or policy, development reflects a coordinated transformation involving structural, institutional, and market-based forces that interact across time and space. Classical economic thought emphasized capital accumulation, labor productivity, and technological progress as core growth determinants, while contemporary approaches increasingly highlight institutional quality, market integration, innovation dynamics, spatial inequalities, and global interdependencies as critical drivers of development outcomes. This conceptual transition from linear to systemic interpretations of economic change underscores the need for analytical models capable of capturing the complexity and interdependence inherent in real-world economic systems.

The role of theoretical and mathematical modeling in understanding growth phenomena has been well recognized in economic literature. Debreu (1984) famously argued that mathematics provides a language for economics that enables precise reasoning, formal abstraction, and analytical clarity. Through mathematical modeling, economists can represent structural relationships and investigate counterfactual scenarios in ways that narrative reasoning alone cannot achieve. In a similar vein, Petrakis (2020) emphasizes that economic growth and development theories benefit from interdisciplinary modeling approaches that combine economics with quantitative, geographical, behavioral, and institutional perspectives. These approaches demonstrate that conceptual and mathematical frameworks do not replace empirical economics but rather enhance its interpretive and predictive capabilities.

In parallel with formal mathematical modeling, conceptual frameworks have played an essential role in structuring economic inquiry. Conceptual frameworks help researchers identify relevant variables, establish theoretical boundaries, and define causal or systemic linkages. For example, Ghadim and Pannell (1999) used conceptual modeling to examine innovation adoption in agricultural contexts, illustrating how behavior, information, and perceived risk shape technology diffusion. Similarly, Ramkissoon (2015) applied a conceptual framework to understand cultural tourism development in African island economies, demonstrating that place-based authenticity, satisfaction, and attachment interact with economic outcomes. At the macroeconomic level, Fusfeld (1980) outlined the conceptual foundations of modern economics to explain how market structure, institutional change, and policy influence national and global economic systems. Together, these examples show that conceptual frameworks serve as bridges between theoretical abstraction and empirical analysis, fostering analytical clarity in complex problem spaces.

Mathematical modeling complements conceptual frameworks by introducing symbolic and computational precision. Vasconcelos (2013) demonstrated how symbolic and numerical models can be used to explore economic growth trajectories, revealing nonlinear patterns and dynamic behavior that traditional verbal models struggle to represent. Debreu (1989) further emphasized that mathematical expression enhances economic content by imposing logical structure, enabling comparison across models, and allowing results to be replicated or extended. The convergence of conceptual and mathematical modeling traditions therefore reflects an ongoing evolution in economics: from discipline-specific reasoning to systemic and interdisciplinary analysis.

It is within this intellectual environment that the present study introduces Economics Equation–3, a symbolic and conceptual model designed to address a central research question: “What policies, structural factors, and economic forces are necessary to transform an economy from low or medium levels to a strong and sustainable state?” While conventional growth theories isolate individual variables—such as capital, labor, or technology—the proposed framework focuses on dynamic interactions between growth-supporting conditions, market flow dynamics, and limiting constraints. This perspective is especially relevant because real economies rarely follow smooth linear trajectories; instead, they evolve through feedback loops, structural bottlenecks, policy shocks, and adaptive changes.

By identifying underlying economic drivers and constraints, the framework highlights how productive capacity, market accessibility, temporal variability, and policy design interact to shape development pathways. For example, workforce motivation, product purity, and domestic sales strength may contribute positively to economic performance, while logistical inefficiencies, demand volatility, and external shocks may offset these gains. The resulting economic outcome depends not merely on improving positive factors but on managing the interaction between enabling and limiting forces. This systems-oriented reasoning aligns with evolutionary and complexity-based economic perspectives that conceptualize economies as adaptive systems rather than mechanical machines (Dopfer, 2005). In evolutionary frameworks, development emerges through processes of variation, selection, and diffusion across firms, industries, and regions—implying that structural change, institutional adaptation, and feedback loops are central to sustainable growth.

Moreover, as economies globalize, market flows are increasingly shaped by spatial and temporal conditions. Consumer behavior varies across demographic segments; place influences logistics, market access, and resource distribution; and time captures seasonal, cyclical, and long-term shifts in demand and policy. Integrating these dimensions into conceptual modeling enables more realistic representations of economic transformation. The Economics Equation–3 framework incorporates these dynamics through its treatment of customers, place, and time as critical modifiers of market flow.

In summary, the Economics Equation–3 framework builds upon longstanding traditions in conceptual economics, mathematical modeling, and evolutionary development theory. It offers a structured approach for analyzing how economies transition from lower developmental stages toward stronger, more resilient states. While the model presented is conceptual and symbolic rather than empirical or predictive, it provides a foundation for future research, simulation, policy evaluation, and strategic planning. Rather than seeking to replace classical growth theories, the framework aims to complement them by emphasizing systemic interactions, constraint management, and adaptive economic dynamics.

2. Methods and Modeling Framework

Figure 1 illustrates the methodological framework employed in this study, outlining the sequential process of factor identification, system flow conceptualization, and symbolic performance modeling. The figure shows how positive growth drivers (A), market flow dynamics (F), and negative constraints (C) interact to influence economic outcomes.

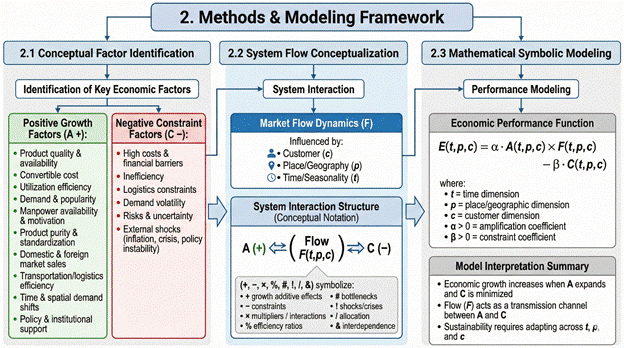
Figure 1: Methodological Framework

2.1 Conceptual Factor Identification

The first methodological stage involved identifying key positive and negative economic factors influencing productivity, market flow, and performance. Drawing from conceptual economic literature and practical development considerations, the following factors were determined to be fundamental:

• product quality and availability, convertible cost, utilization efficiency, demand, manpower and motivation, product purity, domestic and foreign sales ratings, transportation cost, seasonal popularity, temporal and spatial demand shifts, policy support, and contextual externalities.

These reflect broader economic categories such as production capacity, market access, and institutional capability—recognized in both classical and contemporary development theory (Weaver, 1993; Petrakis, 2020).

2.2 System Flow Conceptualization

The economic system is modeled as an interaction among:

• A (+): positive growth factors,
• Flow: market dynamics influenced by customer, place, and time,
• C (−): negative constraints and risks.

This approach aligns with systemic frameworks in evolutionary economics and structural development theory (Dopfer, 2005). Symbolic operators (+, −, ×, %, #, !, /, &) were assigned meaning to represent growth amplification, constraints, multipliers, efficiencies, bottlenecks, shocks, allocations, and interdependencies.

2.3 Mathematical Symbolic Modeling

The economic performance of an entity (firm, sector, or nation) is expressed as:

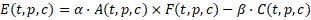
where = time, = place/geography, = customer characteristics.
Positive factors and negative factors are defined as vectors, and flow represents market access modified by time, space, and demand.

This symbolic modeling approach reflects the broader movement of “mathematics serving economics” (Czerwinski, 2024) and Debreu’s mathematical mode of representing economic content (Debreu, 1984).

3. Results

Application of the proposed conceptual structure—Economics Equation–3—provides several meaningful results concerning the nature of economic development, the determinants of economic performance, and the strategic implications for policy and market actors. Although the framework remains theoretical, its symbolic and structural features yield clear insights into how economic growth unfolds within a dynamic environment influenced by productive forces, market flow, and negative constraints.

First, the model reveals that economic growth emerges from interaction rather than isolation. Traditional growth models often emphasize individual factors such as capital accumulation, labor force expansion, or technological advancement. However, the symbolic relationship expressed as demonstrates that a single improved variable—such as product quality, workforce motivation, or manufacturing efficiency—is insufficient to produce sustained gains unless accompanied by favorable conditions in the broader system. For example, high product quality cannot translate into economic strength without market access, competitive pricing, logistics, and policy stability. This systems-based observation aligns with the logic of structural and institutional economics, which argues that development is path-dependent and shaped by multiple interlocking dimensions rather than singular shocks or interventions. The model therefore highlights the importance of complementarity among factors: productivity gains must interact with domestic and international market flows, while policy must facilitate allocation of resources, protection of investment, and mitigation of market failures.

Second, the results indicate that temporal, spatial, and demographic variability significantly influence economic performance. In the model, the flow function is explicitly conditioned by time (seasonal cycles, short vs. long-run dynamics), place (local, national, or international markets), and customer characteristics (income level, demographic composition, cultural preference). This result resonates with empirical findings in regional and development economics, where performance varies across territories due to resource availability, infrastructure, institutional capacity, and demand heterogeneity. Weaver (1993) demonstrated that export performance and growth differ across national contexts depending on external demand, internal constraints, and structural preparedness, illustrating how geographical variation shapes economic trajectories. Similarly, demographic economics emphasizes that demand patterns shift with population age structure, income distribution, and consumption preferences, affecting the magnitude and elasticity of market flows. The framework underscores that economic systems are not temporally uniform or spatially homogeneous, meaning actors—whether firms or governments—must adapt strategies to evolving temporal market cycles, geographic constraints, and evolving consumer needs.

Third, the model demonstrates that negative constraints must be actively addressed because they exert downward pressure on growth momentum. The vector incorporates high costs, logistical inefficiencies, market risks, demand volatility, and external shocks—including inflation, financial crises, or geopolitical instability. These variables contribute to economic friction, reducing the effective output of positive growth drivers. Even if productive capacity and market demand expand, increases in costs, bottlenecks, or uncertainty can neutralize these gains. This result aligns with structural constraint theories in development economics, which argue that infrastructure gaps, institutional rigidities, and volatility impose ceilings on growth potential, particularly in developing economies. The symbolic subtraction term within the model emphasizes that constraints increase as a weighted function of contextual friction, implying the arithmetic of development includes both additive growth forces and subtractive obstacles. Therefore, economic improvement depends not only on amplifying positive forces but also on mitigating or eliminating persistent constraints.

Fourth, the model highlights that policy optimization significantly influences economic outcomes. The relationship between , , , and implies a strategic control problem: governments or institutional actors can maximize economic performance by increasing the magnitude of positive drivers , reducing constraints , and improving the efficiency of flow dynamics through better infrastructure, market access, and temporal coordination. Policy levers may include regulatory reforms, trade agreements, logistics development, workforce training, technology upgrading, institutional strengthening, and stabilization mechanisms against external shocks. The model therefore suggests that policy success derives not from isolated interventions but from coordinated optimization across multiple dimensions.

Collectively, these results reinforce the argument that economic development is a systemic outcome generated by interactions among growth forces, constraints, and adaptive flow dynamics. The symbolic structure of Economics Equation–3 offers a concise representation of these interactions and provides a foundation for analytical, empirical, and simulation-based extensions in future research.

The resulting model yields several structural insights:

1. Economic growth emerges from interaction, not isolation: Improvement in a single variable (e.g., product quality) is insufficient without market access, policy support, and cost efficiency.
2. Temporal, spatial, and demographic variability matter: Performance changes with seasons, geographic markets, and customer income levels—consistent with multi-dimensional growth studies (Weaver, 1993).
3. Negative constraints must be addressed: High costs, logistical bottlenecks, risks, and shocks reduce growth momentum, aligning with structural constraint theories.
4. Policy optimization influences outcomes: Equation terms imply governments can maximize by maximizing , minimizing , and optimizing .

4. Discussion

The results derived from the Economics Equation–3 framework reinforce the idea that economic development is neither linear nor deterministic, but rather emerges from the coordinated interaction of multiple components operating under dynamic conditions. This perspective aligns closely with evolutionary economic theory, which conceptualizes development as a cumulative process characterized by feedback loops, adaptive behavior, and structural change (Dopfer, 2005). Instead of examining isolated causal factors—such as capital, labor, or productivity—the model emphasizes that economic outcomes result from systemic relationships between enabling factors, market flow dynamics, and limiting constraints. This systems-oriented logic challenges traditional reductionist approaches and provides a more realistic representation of how real economies evolve over time.

A central insight from the framework is that strong economies emerge when positive forces (A) expand more rapidly than negative constraints (C), and when market flow (F) remains flexible and responsive to temporal, spatial, and demographic variation. In practical terms, this means that policy efforts aimed solely at enhancing production capacity or improving product quality will not achieve optimal results if logistical bottlenecks, demand volatility, or external shocks remain unaddressed. Conversely, reducing structural constraints without investing in productive capacity will also fail to generate meaningful growth. The model therefore supports an integrated development strategy that simultaneously strengthens productive assets, minimizes constraints, and improves market connectivity.

The incorporation of time, place, and customer characteristics into the flow function reflects an interdisciplinary understanding of economic performance. Time introduces economic cycles, seasonal effects, and long-term transition paths; place introduces spatial heterogeneity, infrastructure differences, and global integration; and customer characteristics introduce preferences, purchasing power, and social stratification. Recognizing these dimensions extends the model beyond traditional macroeconomic abstractions and aligns it with contemporary development literature that emphasizes contextual variability and market segmentation (Petrakis, 2020). Such an approach also holds relevance for firms and industries operating in competitive markets where adaptation to consumer behavior and geographic conditions is essential for survival and growth.

The symbolic and mathematical nature of the model offers advantages for future analytical and empirical extensions. By formalizing the interactions among variables, the framework encourages computational simulation and quantitative sensitivity analysis. This aligns with the broader tradition in economics that views mathematical models as tools for testing theoretical consistency, generating predictions, and exploring counterfactual scenarios (Debreu, 1984). Vasconcelos (2013) demonstrated the value of symbolic and numerical computation in exploring growth trajectories, reinforcing the idea that conceptual economic models can serve as foundations for more detailed numerical analysis. In this sense, the Economics Equation–3 framework provides a conceptual seed that could be operationalized using empirical data, agent-based modeling, or system dynamics simulations.

Finally, the model carries implications for policy design and strategic planning. Governments and institutions can use the framework to identify leverage points where interventions yield the highest returns—such as improving logistics infrastructure, supporting workforce development, or mitigating risks associated with shocks and uncertainty. Because the model distinguishes between growth drivers and constraints, it allows policymakers to target both sides of the development equation. In addition, the emphasis on flow dynamics highlights the importance of aligning production with market reality rather than treating them as separate spheres.

In summary, the Economics Equation–3 framework enriches the conceptual landscape of development economics by bridging systems thinking, mathematical representation, and evolutionary theory. While conceptual and not empirical, it offers a structured basis for future modeling, calibration, and policy-oriented research.

The model supports the notion that economic development is a systemic process shaped by complex interactions, consistent with evolutionary and interdisciplinary frameworks (Dopfer, 2005; Petrakis, 2020). It emphasizes that strong economies emerge when positive forces expand faster than constraints, and when market flow remains adaptive to time, location, and demand. The symbolic approach encourages future numerical calibration and simulation, aligning with the mathematical modeling traditions highlighted by Vasconcelos (2013) and Debreu (1984).

5. Conclusion

The Economics Equation–3 framework presented in this study offers a conceptual and symbolic approach to understanding how economic strength emerges from the interaction among productive forces, market flow dynamics, and negative constraints. Rather than attributing development to a single factor, the model emphasizes the need for alignment between growth-supporting variables—such as product quality, workforce capacity, and policy support—and adaptive market mechanisms shaped by time, location, and customer characteristics. At the same time, the model acknowledges that high costs, logistical bottlenecks, volatility, and systemic shocks exert downward pressure on growth outcomes. The resulting economic performance depends on the degree to which positive drivers expand faster than limitations.

Although theoretical in nature, the model holds value for policy makers, businesses, and academic researchers. For policy makers, it provides a structured means of identifying leverage points for intervention, allowing governments to enhance productive capacity while minimizing structural barriers and external vulnerabilities. For firms and industries, the framework highlights the importance of integrating production strategies with market conditions rather than treating them as isolated domains. For academic researchers, the symbolic configuration creates opportunities for analytical refinement, mathematical formalization, and interdisciplinary dialogue between economics, systems science, and quantitative modeling.

Future research can advance the framework by operationalizing it in several directions. One promising avenue is empirical calibration using sectoral or national datasets to test the sensitivity of performance outcomes to different configurations of productive factors, market flows, and constraints. Another direction involves simulation-based approaches, such as system dynamics or agent-based modeling, which can explore nonlinear trajectories and adaptive behavior under varied policy scenarios. Comparative research across countries or industries may also yield insights into how structural heterogeneity shapes the model’s parameters and predictive reliability.

In summary, Economics Equation–3 provides a foundational conceptual system that invites further development, empirical testing, and policy-oriented application in the field of economic growth and development..

References

Mashrafi, M. (2026). Universal Life Energy–Growth Framework and Equation. International Journal of Research, 13(1), 79-91.

Mashrafi, M. (2026). Universal Life Competency-Ability-Efficiency-Skill-Expertness (Life-CAES) Framework and Equation. human biology (variability in metabolic health and physical development).

Fusfeld, D. R. (1980). The conceptual framework of modern economics. Journal of Economic Issues, 14(1), 1-52.

Vasconcelos, P. B. (2013). Economic growth models: symbolic and numerical computations. Advances in Computer Science: an International Journal, 2(5), 47-54.

Czerwinski, A. (2024). Mathematics serving economics: a historical review of mathematical methods in economics. Symmetry, 16(10), 1271.

Weaver, J. H. (1993). Exports and economic growth in a simultaneous equations model. The Journal of Developing Areas, 27(3), 289-306.

Debreu, G. (1984). Economic theory in the mathematical mode. The American Economic Review, 74(3), 267-278.

Dopfer, K. (2005). Evolutionary economics: a theoretical framework. The evolutionary foundations of economics, 3-55.

Petrakis, P. E. (2020). Theoretical approaches to economic growth and development. An Interdisciplinary Perspective. Switzerland: National and Kapodistrian University of Athens, 26-544.

Debreu, G. (1989). Theoretic models: mathematical form and economic content. In Joan Robinson and Modern Economic Theory (pp. 264-277). London: Palgrave Macmillan UK.

Ramkissoon, H. (2015). Authenticity, satisfaction, and place attachment: A conceptual framework for cultural tourism in African island economies. Development Southern Africa, 32(3), 292-302.

Ghadim, A. K. A., & Pannell, D. J. (1999). A conceptual framework of adoption of an agricultural innovation. Agricultural economics, 21(2), 145-154.