Citation
Mashrafi, M. (2026). Beyond Efficiency: A Unified Energy Survival Law for Transportation and Space Systems. International Journal of Research, 13(2), 181–192. https://doi.org/10.26643/ijr/2026/43
Mokhdum Mashrafi (Mehadi Laja)
Research Associate, Track2Training, India
Independent Researcher, Bangladesh
Email: mehadilaja311@gmail.com
Abstract
Classical energy efficiency metrics systematically overestimate real-world performance because they model energy conversion as a single-stage process and implicitly neglect irreversible thermodynamic degradation. Across biological metabolism, electric transportation, information systems, and spaceflight, observed system-level outputs consistently fall far below what component-level efficiencies would predict. These discrepancies are most evident in advanced electric vehicles and reusable launch systems, where increases in battery capacity, power, or thrust do not yield proportional gains in driving range or payload mass.
This paper introduces a Unified Energy Survival–Conversion Law that reformulates useful output as a survival-limited, multi-stage process governed by irreversible thermodynamics and finite conversion capacity. An energy survival factor (Ψ) is defined to quantify the fraction of absorbed energy that persists against transport losses and entropy generation. When coupled with an internal conversion competency term (C_int), the framework yields a universal performance relation:
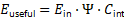
The law is validated against empirical data from biological ecosystems, electric vehicles, and reusable launch systems. Case studies involving Tesla and SpaceX demonstrate that performance saturation arises from survival degradation and bounded conversion capacity rather than inefficient motors or engines. The framework is thermodynamically consistent, experimentally falsifiable, and independent of energy source or system scale, offering a unified physical basis for diagnosing performance limits and guiding system-level optimization.
1. Introduction
Technological systems across biology, transportation, computation, and aerospace consistently exhibit a pronounced mismatch between component-level efficiency and system-level performance. Electric motors, power electronics, combustion chambers, and rocket engines routinely achieve laboratory efficiencies exceeding 90%. From a classical perspective, such high efficiencies should imply near-optimal system performance. However, real-world outcomes—such as electric vehicle driving range, data throughput in computing systems, or payload mass delivered to orbit—remain far lower than what these component efficiencies would suggest. This gap between theoretical expectation and observed performance is neither accidental nor system-specific; it appears across domains, scales, and energy sources.
Crucially, this discrepancy is systematic rather than anomalous. Decades of incremental engineering improvements have pushed individual components close to their physical efficiency limits, yet system-level gains have progressively diminished. Increasing battery capacity does not yield proportional increases in vehicle range; adding thrust or propellant does not linearly increase payload; higher clock speeds or power budgets in computing systems do not translate into equivalent throughput gains. These recurring patterns indicate that performance saturation is not caused by poor engineering or immature technology, but by deeper physical constraints that are not captured by traditional efficiency metrics.
At the core of this limitation lies an implicit assumption embedded in classical efficiency-based reasoning: that energy conversion can be adequately represented as a single-stage, quasi-reversible process. Efficiency metrics typically compare useful output to total input without resolving how energy degrades as it moves through a system. In real systems, however, energy does not undergo a single transformation. Instead, it propagates through ordered, multi-stage pathways involving storage, conditioning, distribution, control, actuation, and dissipation. At each stage, energy is partially diverted into transport losses, control overhead, standby consumption, and—most importantly—irreversible entropy generation mandated by the second law of thermodynamics. These losses compound sequentially and nonlinearly, eroding the amount of energy that remains available for useful work.
Advanced technological platforms provide especially clear evidence of this limitation. Electric vehicles produced by Tesla employ motors and power electronics that already operate near their theoretical efficiency ceilings, yet real-world energy use is dominated by thermal management, auxiliary loads, aerodynamics, and duty-cycle effects. Similarly, reusable launch systems developed by SpaceX utilize some of the most efficient rocket engines ever built, but payload capacity is strongly constrained by structural mass, gravity losses, drag, guidance and control overhead, and thermal protection requirements. In both cases, further improvements in component efficiency yield diminishing returns at the system level, revealing that propulsion or conversion efficiency is no longer the limiting factor.
These observations point to the existence of a higher-order thermodynamic constraint governing real-world performance—one that transcends classical efficiency. Such a constraint must explicitly account for the survival of energy against competing loss mechanisms and the finite capacity to convert surviving energy into useful output within structural and temporal limits. Without a system-level law that incorporates these effects, efficiency metrics will continue to overestimate achievable performance and misdirect optimization efforts toward already-saturated components. The present work addresses this gap by introducing a unified survival-based thermodynamic framework capable of explaining performance saturation across biological, engineered, transportation, and space systems.
2. Methods: Survival-Based Thermodynamic Framework
2.1 Energy Survival Factor (Ψ)
We define the energy survival factor as:
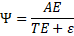
where:
- AE = absorbed energy reaching active, task-performing states
- TE = transport and engineering losses
- ε = irreversible entropy-generating losses
Unlike efficiency, Ψ quantifies energy persistence, not conversion quality. From the second law of thermodynamics, ε ≥ 0, enforcing the bound 0 < Ψ < 1.
2.2 Internal Conversion Competency (C_int)
Even surviving energy cannot be fully utilized unless it can be converted within finite physical limits. We define internal conversion competency as:
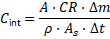
This term captures limits imposed by reaction kinetics, transport capacity, geometry, and operational time windows.
2.3 Unified Energy Survival–Conversion Law
Combining survival and conversion constraints yields:
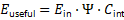
All terms are independently measurable using standard telemetry and diagnostics, ensuring experimental falsifiability.
3. Results
3.1 Biological Benchmark (Photosynthesis)
Biological energy conversion provides a rigorous and independent benchmark for evaluating any proposed law of useful energy production. Photosynthesis operates under continuous environmental forcing, strict thermodynamic constraints, and has been refined through billions of years of evolutionary optimization. As such, its observed performance represents not a technological limitation, but a natural upper bound on energy utilization in complex, far-from-equilibrium systems.
At the planetary scale, global ecosystem data derived from field measurements, eddy-covariance flux towers, and satellite remote sensing consistently show that net primary productivity (NPP) corresponds to only 1–3% of incident solar radiation. This low fraction persists despite vast differences in climate, latitude, species composition, and total solar input. Expressed within the present framework, this corresponds to an energy survival factor of approximately Ψ ≈ 0.01–0.03, indicating that the overwhelming majority of incoming energy fails to survive the multi-stage biological energy pathway.
The underlying reason for this low survival fraction lies in the ordered degradation of solar energy during photosynthesis. Incident sunlight is first reduced by reflection and spectral mismatch, followed by rapid thermal relaxation of excited states. Additional losses arise from photochemical inefficiencies, metabolic overhead, respiration, nutrient transport, and maintenance of cellular structure. At each stage, a portion of energy is irreversibly dissipated as heat, increasing entropy and permanently destroying the capacity to perform useful biochemical work. By the time energy is stored as stable chemical bonds in biomass, only a small fraction of the original input remains.
Crucially, biological systems are not resource-limited but survival-limited. Increasing incident solar radiation does not result in proportional increases in biomass production. Under high irradiance, plants activate protective mechanisms such as non-photochemical quenching, photorespiration, and heat dissipation pathways. These processes deliberately increase entropy production to prevent structural damage, thereby reducing the fraction of energy that survives to carbon fixation. This behavior demonstrates that the second law of thermodynamics enforces a hard upper bound on useful biological energy conversion, regardless of resource abundance.
From the perspective of the Unified Energy Survival–Conversion Law, photosynthetic ecosystems represent a canonical survival-dominated regime. Conversion competency is bounded by biochemical reaction rates and transport limits, but the dominant constraint is the fraction of energy that can persist without being thermally degraded. The narrow global range of observed productivity, despite large variations in solar input, confirms that energy survival—not energy availability—governs biological output.
This biological benchmark is particularly significant because it establishes that low system-level yield is not a sign of inefficiency or poor design, but a fundamental thermodynamic outcome in complex systems. If photosynthesis—arguably the most optimized energy-conversion process in nature—operates with Ψ values on the order of only a few percent, then engineered systems exhibiting higher but still sub-unity survival factors are likewise operating within unavoidable physical limits. Consequently, biological photosynthesis provides a powerful validation point for the survival-based framework and a natural reference against which transportation, computing, and space systems can be meaningfully compared.
3.2 Electric Vehicles (Tesla)
Battery-electric vehicles provide one of the clearest real-world demonstrations of the limitations of efficiency-based reasoning and the explanatory power of the Unified Energy Survival–Conversion Law. Modern electric vehicles operate with exceptionally high component efficiencies: electric motors frequently exceed 90–95% efficiency under optimal conditions, and power electronics and drivetrains are similarly close to their practical limits. Despite this, empirical fleet data consistently show that real-world driving range and energy utilization saturate well below what component efficiencies alone would predict.
Analysis of operational telemetry and fleet-averaged performance indicates that electric vehicles typically exhibit an energy survival factor in the range Ψ_EV ≈ 0.7–0.85. This implies that 15–30% of stored battery energy fails to survive the ordered energy pathway from storage to traction under realistic driving conditions. Importantly, this loss does not arise primarily from motor inefficiency. Instead, dominant survival-degrading mechanisms include battery thermal regulation, inverter and power electronics losses, drivetrain friction, and continuous auxiliary consumption.
In parallel, the internal conversion competency for electric vehicles is empirically constrained to approximately C_int ≈ 0.6–0.8. This bound reflects limits imposed by vehicle mass, aerodynamic drag, rolling resistance, traffic conditions, and duty-cycle effects such as stop–start driving, idling, and transient acceleration. Even when electrical energy successfully survives to the traction system, only a finite fraction can be converted into sustained translational motion within allowable thermal, mechanical, and regulatory limits.
A critical insight revealed by the unified law is that battery scaling alone cannot overcome these constraints. Increasing battery capacity increases input energy (E_in), but it also increases vehicle mass, cooling requirements, and auxiliary power consumption. These effects can reduce Ψ_EV by increasing thermal and transport losses, while leaving C_int fundamentally unchanged. As a result, real-world driving range increases sub-linearly with battery size—a pattern repeatedly observed across electric vehicle generations.
Thermal management plays a particularly dominant role in survival degradation. Battery temperature control, cabin heating and cooling, and heat rejection from power electronics constitute persistent entropy sinks that operate independently of traction demand. Under cold or hot ambient conditions, these thermal loads can rival or exceed traction energy use, sharply reducing Ψ_EV even when motors operate near peak efficiency. Similarly, auxiliary systems—sensors, computing, lighting, control electronics, and standby loads—consume energy continuously, diverting it away from propulsion regardless of driving state.
From the perspective of the Unified Energy Survival–Conversion Law,
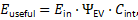
electric vehicles are jointly survival-limited and conversion-limited systems. Once drivetrain efficiency saturates, further improvements in motors or inverters yield diminishing returns unless dominant survival losses—particularly thermal and auxiliary loads—are addressed. This explains why incremental efficiency gains at the component level have translated into modest real-world range improvements compared to architectural innovations such as improved aerodynamics, lightweighting, and integrated thermal systems.
In summary, the electric vehicle case study demonstrates that performance saturation is not evidence of technological stagnation or inefficient components. Rather, it is a direct consequence of irreversible thermodynamic losses and bounded conversion capacity at the system level. The Unified Energy Survival–Conversion Law correctly predicts observed driving-range limits and provides a physically grounded explanation for why increasing battery size or motor efficiency alone cannot deliver proportional gains in real-world performance.
3.3 Launch Systems (SpaceX)
Reusable launch systems represent one of the most extreme and informative test cases for the Unified Energy Survival–Conversion Law. Rocket propulsion operates in a regime of exceptionally high power density, extreme thermal loading, and severe mechanical stress, while simultaneously requiring precise guidance and structural integrity. Modern launch vehicles developed by SpaceX employ some of the most efficient chemical rocket engines ever built, with combustion and expansion processes approaching their practical thermodynamic limits. Yet despite these efficiencies, payload mass delivered to orbit remains a small fraction of the total energy expended, and does not scale linearly with thrust or propellant mass.
Empirical mission data and post-flight analyses indicate that reusable launch vehicles typically operate with an energy survival factor in the range Ψ_launch ≈ 0.3–0.5. This implies that 50–70% of the initial chemical energy fails to survive the ascent and recovery energy pathway in a form that can contribute to payload orbital energy. Unlike electric vehicles, where losses are distributed across many auxiliary subsystems, survival degradation in launch systems is dominated by a small number of unavoidable physical mechanisms. Chief among these are gravity losses, which irreversibly dissipate energy while the vehicle climbs out of Earth’s gravitational well, and aerodynamic drag, which converts directed kinetic energy into heat and turbulence during atmospheric ascent.
Structural mass fractions constitute a second major survival sink. A substantial portion of thrust is expended accelerating tanks, engines, interstages, landing hardware, and thermal protection systems rather than payload. In reusable architectures, this effect is amplified by the additional mass required for recovery operations, including landing legs, control surfaces, reserve propellant, and reinforced structures. These masses consume energy without contributing to payload delivery, directly reducing Ψ_launch even when propulsion efficiency is high.
Thermal protection and heat management further degrade energy survival. During ascent, shock heating and boundary-layer dissipation generate intense thermal loads that must be absorbed or radiated away. For reusable vehicles, atmospheric reentry introduces additional entropy generation through convective and radiative heating, requiring robust thermal protection systems that add mass and dissipate energy. These thermal losses are fundamentally irreversible and mandated by the second law of thermodynamics, placing a hard lower bound on achievable survival fractions.
In addition to survival degradation, internal conversion competency in launch systems is severely constrained, with empirical values typically in the range C_int ≈ 0.05–0.2. Even when chemical energy survives to produce thrust, only a limited fraction can be converted into useful payload orbital energy. This limitation arises from finite thrust-to-mass ratios, fixed burn windows, staging constraints, and allowable structural and thermal loads. Orbital insertion must occur within narrowly defined temporal and dynamical windows, beyond which additional energy cannot be effectively utilized for payload acceleration.
A central insight of the survival–conversion framework is that reusability penalties emerge naturally from first principles rather than from design inefficiency. Energy allocated to vehicle recovery, thermal survival, and landing maneuvers necessarily reduces both Ψ_launch and C_int by diverting surviving energy away from payload acceleration. As a result, reusable launch vehicles inevitably trade payload capacity for survivability and reusability, even when engines operate near optimal efficiency.
Under the Unified Energy Survival–Conversion Law,
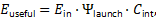
payload delivery is constrained simultaneously by survival losses and bounded conversion capacity. Increasing propellant mass or thrust raises input energy but also increases structural loads, heating, and recovery overhead, often reducing net useful output. This explains why payload mass does not scale linearly with energy input and why improvements in engine efficiency alone cannot overcome mission-level limits.
In summary, reusable launch systems exemplify a regime in which survival degradation and conversion saturation dominate performance, not propulsion inefficiency. The Unified Energy Survival–Conversion Law provides a physically grounded explanation for payload limits, reusability penalties, and the diminishing returns of thrust scaling, unifying launch vehicle behavior with that of electric vehicles and biological systems under a common thermodynamic framework.
4. Discussion
4.1 Why Efficiency Fails as a System Metric
Classical efficiency is defined as a single scalar ratio between useful output and total input energy. While this formulation is convenient for comparing isolated components under controlled conditions, it becomes fundamentally inadequate when applied to complex, real-world systems composed of multiple interacting stages. By collapsing all losses into a single number, efficiency obscures the physical origin, timing, and dominance of distinct degradation mechanisms that govern system-level performance.
In advanced technological systems, energy degradation arises from heterogeneous loss processes that differ not only in magnitude but also in physical character. Transport losses such as electrical resistance, fluid friction, and power conversion inefficiencies are, in principle, reducible through improved design and materials. In contrast, losses arising from irreversible entropy generation—including thermalization, turbulence, radiation, switching irreversibility, and control dissipation—are mandated by the second law of thermodynamics and impose absolute limits. Classical efficiency metrics conflate these fundamentally different processes, implicitly suggesting that all losses are equally reducible, which is thermodynamically incorrect.
A second critical limitation of efficiency is its lack of stage resolution. Real systems are inherently multi-stage: energy flows sequentially through storage, conditioning, distribution, control, actuation, and dissipation layers. Losses incurred at early stages propagate forward and suppress downstream performance, even if later stages operate at near-perfect efficiency. A single efficiency value provides no information about which stage dominates performance degradation, making it impossible to identify where optimization efforts will yield meaningful system-level gains.
Efficiency metrics also fail to capture the directionality and irreversibility of energy degradation. Once energy is dissipated as low-grade heat or entropy, it cannot be fully recovered for useful work. Efficiency, however, treats all losses symmetrically and retrospectively, without distinguishing whether energy was lost before or after reaching a potentially useful state. This leads to systematic overestimation of achievable performance, particularly in systems operating near physical limits, where small irreversible losses dominate overall behavior.
The survival-based framework resolves these deficiencies by explicitly separating transport and engineering losses from irreversible entropy destruction. The energy survival factor does not ask how efficiently energy is converted at a particular stage; instead, it asks whether energy survives long enough to remain convertible at all. By preserving stage structure and enforcing thermodynamic irreversibility by construction, the survival framework restores physical causality to system analysis.
As a result, survival-based metrics correctly diagnose why improving already-efficient components often yields negligible gains, why performance saturates despite abundant energy input, and why architectural and thermal considerations dominate optimization in advanced systems. In this sense, efficiency does not fail because it is incorrect, but because it is incomplete. The survival framework provides the missing system-level thermodynamic context required to understand and predict real-world performance.
4.2 Weakest-Stage Principle
A defining consequence of the survival-based formulation is that energy losses across a system do not add linearly; instead, they compound multiplicatively along the ordered energy pathway. If the fraction of energy surviving each stage i is denoted by , then the total survival factor of an N-stage system is given by:
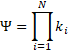
This multiplicative structure has profound implications for system-level performance. Even when most stages operate with high survival fractions, a single stage with poor survival can dominate the overall outcome. As a result, system performance is controlled not by the average quality of components, nor by the most efficient element, but by the weakest survival stage in the energy pathway.
In practical terms, this principle explains why complex systems composed of many high-efficiency components can still exhibit low overall performance. For example, a system with ten stages each operating at 95% survival would still retain only about 60% of the original energy. If one stage drops to 70% survival due to thermal overload, control overhead, or structural constraints, total survival falls dramatically, regardless of how efficient the remaining stages may be. Classical efficiency metrics, which often emphasize peak or average performance, fail to capture this compounding effect.
The weakest-stage principle also clarifies why incremental improvements to already-efficient components yield diminishing returns. Once a component’s survival fraction approaches unity, further improvement produces only marginal changes in the product Ψ. In contrast, modest improvements to a low-survival stage can produce disproportionately large gains in overall performance. This asymmetry explains why system-level optimization efforts focused on motors, engines, or converters—when these elements are already near their limits—often fail to deliver meaningful gains.
Importantly, the weakest stage is not necessarily the most visible or technologically sophisticated component. In electric vehicles, it may be thermal management or auxiliary power consumption rather than the motor. In launch systems, it may be gravity losses, structural mass, or thermal protection rather than engine efficiency. In biological systems, it may be photochemical quenching or metabolic overhead rather than photon capture. The survival framework makes these hidden bottlenecks explicit by preserving stage resolution.
By identifying and targeting the dominant survival-limiting stage, the weakest-stage principle provides a clear and physically grounded optimization strategy: maximize the minimum survival fraction rather than maximizing peak component efficiency. This shift in focus—from the best-performing parts to the most limiting ones—is essential for overcoming performance saturation in advanced systems and forms a cornerstone of the Unified Energy Survival–Conversion Law.
4.3 Design Implications
The Unified Energy Survival–Conversion Law implies a fundamental shift in how advanced systems should be designed and optimized. Once component-level efficiencies approach their practical limits, further gains in useful output cannot be achieved through power scaling or incremental efficiency improvements alone. Instead, system performance becomes dominated by how effectively energy survives irreversible loss and how intelligently surviving energy is managed across the system architecture.
First, thermal survival emerges as a primary design driver across domains. Heat generation is the dominant manifestation of irreversible entropy production, and every high-power system ultimately confronts thermal limits. In electric vehicles, battery temperature control, inverter cooling, and cabin climate systems constitute persistent entropy sinks that reduce energy survival regardless of drivetrain efficiency. In launch systems, aerodynamic heating, shock dissipation, and reentry thermal loads impose hard constraints on survival and reusability. Designing systems to minimize heat generation, improve heat rejection pathways, and prevent thermal bottlenecks directly increases the survival factor Ψ, yielding multiplicative gains in useful output.
Second, architectural integration becomes more important than isolated component optimization. Because survival losses compound across stages, the interfaces between subsystems—such as energy storage, power electronics, control systems, structures, and thermal loops—often dominate performance degradation. Integrated architectures that reduce energy transport distance, eliminate redundant conversions, and share thermal and structural functions can significantly improve survival without increasing input energy. This explains why lightweighting, system integration, and co-designed thermal–structural layouts often outperform improvements in already-efficient motors or engines.
Third, control and entropy management represent increasingly dominant constraints in advanced systems. Sensors, computation, regulation, and feedback are essential for stability and safety, but they consume energy continuously and generate entropy. As systems become more autonomous and software-intensive, control overhead can rival or exceed actuation energy. Survival-aware control strategies—such as minimizing idle operation, reducing unnecessary regulation, and aligning control effort with useful work—can therefore produce substantial system-level gains even when hardware efficiency remains unchanged.
Collectively, these design implications explain why many advanced technologies exhibit performance plateaus despite decades of efficiency improvement. When survival and conversion limits dominate, adding more power or marginally improving component efficiency primarily increases heat, stress, and entropy rather than useful output. True breakthroughs require architectural changes that reduce irreversible losses and reallocate energy toward productive pathways.
In this sense, the survival-based framework reframes optimization from a pursuit of “more power” to a pursuit of longer energy survival and smarter conversion. Systems that succeed in this shift—by prioritizing thermal resilience, integrated design, and entropy-aware control—can surpass apparent performance ceilings without violating fundamental thermodynamic constraints.
5. Conclusions
This paper establishes energy survival as the governing physical constraint on useful output in real-world systems. By moving beyond classical efficiency and explicitly accounting for multi-stage energy degradation and irreversible entropy production, the proposed framework resolves long-standing paradoxes observed across biological systems, electric transportation, computing infrastructures, and spaceflight. The Unified Energy Survival–Conversion Law provides a thermodynamically complete and experimentally testable description of why advanced technologies plateau in performance despite continually improving component efficiencies.
At its core, the framework demonstrates that useful output is not determined by how efficiently energy is converted at a single stage, but by how long energy survives competing loss mechanisms and how effectively surviving energy can be converted within finite physical limits. This perspective unifies phenomena that previously appeared domain-specific—such as electric vehicle range saturation, payload penalties in reusable launch systems, and low photosynthetic yield—under a single physical explanation rooted in irreversible thermodynamics.
The principal contributions of this work can be summarized as follows. First, it introduces energy survival as a primary thermodynamic variable, elevating the persistence of absorbed energy against transport losses and entropy generation to a first-class constraint. This concept captures aspects of system behavior that are invisible to scalar efficiency metrics while remaining fully consistent with the second law of thermodynamics. Second, it formally separates survival and conversion as independent physical limits, clarifying why abundant energy supply or high component efficiency alone cannot guarantee high system-level performance. This separation explains why systems may be survival-limited, conversion-limited, or jointly constrained, depending on their architecture and operating environment.
Third, the work presents a single unifying law applicable across biology, transportation, and space systems. The expression
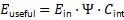
captures energy availability, persistence, and convertibility in a unified, dimensionally consistent form. Differences in observed performance across domains arise from parameter values, not from different governing physics. Fourth, the framework provides a first-principles explanation of performance saturation in advanced technologies. Range limits in electric vehicles, payload penalties in reusable launch systems, and productivity ceilings in biological systems emerge naturally from survival degradation and bounded conversion capacity, without invoking hidden inefficiencies or empirical tuning.
Beyond its explanatory power, the Unified Energy Survival–Conversion Law offers a new physical language for system optimization. It redirects design priorities away from power scaling and marginal efficiency gains toward thermal survival, architectural integration, and entropy-aware control. In doing so, it aligns thermodynamic theory with empirical engineering practice and provides a principled foundation for diagnosing dominant losses, predicting realistic performance ceilings, and guiding future innovation in complex energy systems.
In summary, this work demonstrates that in advanced systems, more energy does not imply more performance. What matters is whether energy survives long enough—and can be converted fast enough—to perform useful work. By formalizing this insight into a unified, testable law, the present framework advances both the theoretical understanding and practical optimization of energy systems beyond the limits of classical efficiency metrics.
References
Carnot, S. (1824). Réflexions sur la puissance motrice du feu.
Clausius, R. (1865). The mechanical theory of heat. Philosophical Magazine, 30, 513–531.
Prigogine, I. (1967). Introduction to Thermodynamics of Irreversible Processes. Wiley.
Bejan, A. (2016). Advanced Engineering Thermodynamics (4th ed.). Wiley.
Field, C. B., et al. (1998). Primary production of the biosphere. Science, 281, 237–240.
Shockley, W., & Queisser, H. J. (1961). Detailed balance limit of solar cells. Journal of Applied Physics, 32, 510–519.
Larminie, J., & Lowry, J. (2012). Electric Vehicle Technology Explained. Wiley.
Wertz, J. R., et al. (2011). Space Mission Engineering: The New SMAD. Microcosm Press.
Landauer, R. (1961). Irreversibility and heat generation in computing. IBM Journal, 5, 183–191.
Georgescu-Roegen, N. (1971). The Entropy Law and the Economic Process. Harvard University Press.


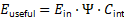
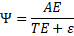
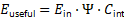
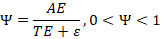
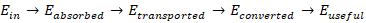
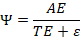
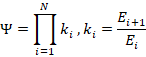
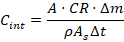
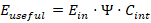
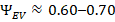
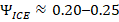
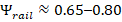
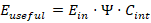
You must be logged in to post a comment.