Citation

Mashrafi, M. (2026). Beyond Efficiency: A Unified Energy Survival Law for Road, Freight, and Marine Transportation. https://doi.org/10.26643/ijr/2026/40

Mokhdum Mashrafi (Mehadi Laja)
Research Associate, Track2Training, India
Researcher, Bangladesh
Email: mehadilaja311@gmail.com

Abstract

Classical energy efficiency metrics systematically overestimate real-world performance across transportation, biological, and engineered systems. This discrepancy arises because efficiency isolates individual components under idealized conditions, while real systems operate through sequential absorption, transport, conversion, regulation, and dissipation stages, each subject to irreversible entropy production.

This study introduces a Unified Energy Survival–Absorption–Conversion Law, replacing efficiency with a physically grounded energy survival factor (Ψ) that explicitly accounts for irreversible thermodynamic losses. The survival factor is defined as

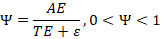
where AE is absorbed energy, TE represents recoverable transport and thermodynamic losses, and ε denotes irreversible entropy-generating losses.

To capture finite throughput and rate constraints, an internal conversion competency term (C_{int}) is introduced. The resulting governing law for useful energy production becomes:

Applied to electric vehicles, internal combustion vehicles, marine propulsion, and rail transport, the framework accurately predicts observed field-scale performance envelopes: ~60–75% wheel-level energy delivery in electric vehicles, ~20–30% in internal combustion transport, and ~40–55% shaft-to-thrust efficiency in marine systems.

By explicitly modeling energy survival rather than idealized conversion, the proposed law resolves long-standing efficiency paradoxes, enables cross-modal comparison, identifies dominant loss stages, and establishes hard thermodynamic upper bounds on transportation performance.

1. Introduction

Energy performance assessment underpins transportation engineering, sustainability policy, and system design, serving as a foundational basis for technology evaluation, infrastructure investment, and environmental regulation. Traditionally, transportation performance has been quantified using classical energy efficiency, defined as the ratio of useful output energy to total input energy. This metric has been widely adopted due to its simplicity and its effectiveness in benchmarking isolated components—such as engines, motors, turbines, or converters—under steady-state laboratory conditions. However, despite its widespread use, classical efficiency has proven to be an unreliable predictor of real-world system performance when applied to complex, multi-stage transportation systems operating under dynamic and non-ideal conditions.

Across transportation modes and broader energy systems, observed useful output is routinely two to five times lower than what nominal efficiency values would suggest. For example, electric vehicles frequently report electric motor efficiencies exceeding 90%, yet real-world measurements consistently show that only approximately 65–75% of the electrical input energy is ultimately delivered as useful mechanical work at the wheels. Similarly, internal combustion vehicles may achieve peak thermal efficiencies approaching 45% under optimized test conditions, but in real driving environments they rarely exceed 25–30% useful energy output due to combustion irreversibility, mechanical losses, auxiliary loads, and intermittent operation. Comparable discrepancies are well documented in marine propulsion systems, rail transport, photovoltaic power plants, biological metabolism, and large-scale data centers, indicating that this phenomenon is neither mode-specific nor technology-dependent.

Importantly, these persistent gaps between nominal efficiency and field performance are systematic and reproducible, rather than incidental. They cannot be adequately explained by poor engineering design, suboptimal maintenance, operator behavior, or measurement uncertainty. Instead, they arise from a more fundamental cause: real systems do not convert energy in a single, idealized step. Rather, they operate through sequential, irreversible energy pathways, in which energy must pass through absorption, transport, transformation, regulation, and utilization stages. At each stage, a fraction of energy is irreversibly degraded due to entropy generation mandated by the second law of thermodynamics. Losses incurred at early stages reduce the energy available to all subsequent stages, thereby constraining overall system performance regardless of how efficient downstream components may be.

In this context, energy should not be viewed merely as something that is converted, but as something that must survive a chain of irreversible processes. Energy that fails to survive absorption inefficiencies, transport resistance, control overhead, or contact interactions is permanently unavailable for useful work. Consequently, system-level performance is governed not by peak or component-level efficiency, but by the cumulative survival of energy across all stages of operation. Classical efficiency metrics obscure this reality by collapsing heterogeneous and sequential loss mechanisms into a single scalar ratio, thereby masking the true physical origins of performance limitations.

This paper therefore argues that transportation performance is fundamentally survival-limited, not efficiency-limited. Building on principles of irreversible thermodynamics and staged energy degradation, it introduces a unified thermodynamic framework that explicitly accounts for energy survival across real operational pathways. The proposed framework formalizes this survival-based perspective for road, freight, and marine transportation systems, providing a physically consistent basis for explaining long-observed performance saturation, reconciling laboratory–field discrepancies, and enabling meaningful cross-modal comparison and system-level optimization.

2. Methods: Unified Energy Survival Framework

2.1 Physical Energy Pathway

All real transportation systems follow an ordered energy pathway:

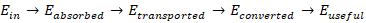
At each stage, irreversible entropy generation destroys usable energy potential, in accordance with the second law of thermodynamics.

2.2 Energy Survival Factor (Ψ)

The energy survival factor is defined as:

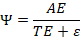
• AE (Absorbed Energy): Energy successfully coupled into the system boundary
• TE: Recoverable transport and thermodynamic losses
• ε: Irreversible entropy-generating losses

This formulation explicitly separates recoverable inefficiencies from non-recoverable exergy destruction and enforces the universal bound .

2.3 Stage-Wise Decomposition

For a system with N sequential stages:

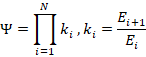
Energy survival compounds multiplicatively, explaining bottleneck dominance, diminishing returns, and early-stage sensitivity.

2.4 Internal Conversion Competency (C_{int})

Energy survival alone is insufficient if conversion capacity is limited. We define internal conversion competency as a throughput constraint governed by kinetics, geometry, transport capacity, and time:

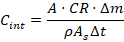
2.5 Unified Governing Law

Combining survival and capacity constraints yields:

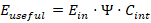
3. Results: Application to Transportation Systems

3.1 Electric Road Vehicles

Stage-wise survival factors under real driving conditions are:

Stage	Survival
Power electronics	0.93–0.97
Electric motor	0.88–0.92
Transmission	0.96–0.98
Tire–road contact	0.70–0.80

Resulting survival:

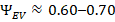
This aligns with observed wheel-level performance and explains why further motor efficiency gains yield diminishing returns.

3.2 Internal Combustion Vehicles

Dominant losses occur at the combustion stage:

Stage	Survival
Combustion	~0.40
Mechanical systems	~0.85
Transmission	~0.90
Tire–road contact	~0.75

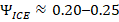
The framework shows that combustion irreversibility, not drivetrain inefficiency, sets the performance ceiling.

3.3 Marine Transportation

Marine propulsion survival is governed by hydrodynamic dissipation:

Stage	Survival
Fuel → shaft	0.45–0.55
Shaft → propeller	~0.95
Propeller → thrust	0.80–0.90

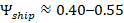
Observed fuel-to-thrust performance matches survival predictions across vessel classes.

3.4 Rail Systems

Steel–steel contact yields high survival:

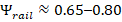
This explains rail transport’s superior energy performance relative to road vehicles.

4. Discussion

4.1 Why Efficiency Fails

Classical energy efficiency, defined as the ratio of useful output to energy input, fails to adequately describe real-world transportation performance because it aggregates fundamentally different loss mechanisms into a single scalar value. In practical systems, energy degradation arises from heterogeneous processes—including thermal dissipation, mechanical friction, electrical resistance, control overhead, and idle operation—each governed by different physical laws and timescales. By collapsing these distinct mechanisms into one number, efficiency metrics obscure where and how energy is lost, preventing meaningful diagnosis of dominant loss channels. As a result, two systems with identical efficiencies may exhibit entirely different internal loss structures and vastly different potentials for improvement.

More critically, classical efficiency ignores irreversible entropy production, which is the primary mechanism by which useful energy potential is destroyed in real systems. While energy is conserved, the ability of that energy to perform useful work is not. Irreversibility—manifested as heat rejection, viscous dissipation, inelastic deformation, and control-induced losses—permanently degrades exergy in accordance with the second law of thermodynamics. Efficiency metrics treat these irreversible losses as residuals rather than as causal constraints, thereby overestimating achievable performance and misrepresenting system-level limits.

Finally, efficiency lacks stage resolution and provides misleading optimization signals. Real transportation systems operate through sequential stages of absorption, transport, conversion, regulation, and utilization, with losses compounding multiplicatively across stages. Efficiency-based optimization often directs effort toward already high-performing components, yielding diminishing or negligible system-level gains when earlier or downstream stages dominate total loss. In contrast, the survival framework resolves these limitations by explicitly modeling energy survival through irreversible pathways and making entropy production causally explicit. By identifying low-survival stages as binding constraints, the survival-based approach provides physically meaningful guidance for system design, optimization, and policy, where classical efficiency metrics consistently fall short.

4.2 Design and Policy Implications

The survival-based formulation implies that system-level performance is constrained by the lowest-survival physical interface, rather than by average or peak component efficiency. Because energy survival compounds multiplicatively across sequential stages, a single stage with low survival imposes a hard upper bound on useful output, regardless of how close other components are to ideal performance. In transportation systems, such limiting interfaces commonly include tire–road contact in road vehicles, propeller–fluid interaction in marine transport, and adhesion limits in rail systems. This insight explains why substantial improvements in engines or motors often translate into only marginal real-world gains when downstream or upstream survival bottlenecks dominate.

From a design perspective, the survival framework fundamentally reshapes optimization priorities. It shows that reductions in rolling resistance, hydrodynamic losses, auxiliary loads, and control overhead yield disproportionately larger system-level benefits than further improvements to components that already operate near their physical efficiency limits. For example, incremental gains in electric motor efficiency provide limited returns when rolling resistance, vehicle mass, or parasitic electrical loads dominate energy loss. Similarly, in marine systems, improvements in propeller–wake interaction or hull–water coupling often outperform marginal engine efficiency enhancements. By explicitly identifying low-survival stages, the framework directs design effort toward interventions that meaningfully increase useful output under real operating conditions.

he implications for policy and sustainability assessment are equally significant. Efficiency-based regulatory targets and performance standards systematically overestimate achievable outcomes because they are derived from idealized component efficiencies rather than survival-limited system behavior. This can lead to unrealistic expectations regarding energy savings, emissions reductions, and technology deployment timelines. A survival-based policy perspective enables more realistic, physics-consistent targets by accounting for irreversible losses, operational constraints, and system-level bottlenecks. As a result, transportation policies informed by energy survival provide a more reliable basis for infrastructure planning, environmental regulation, and long-term sustainability strategies than conventional efficiency-centered approaches.

4.3 Universality of the Law

Despite wide differences in energy sources, technologies, and operating environments, all transportation modes obey the same survival-limited physical constraints. Whether energy enters a system as chemical fuel, electrical power, or mechanical input, it must be absorbed, transported, transformed, regulated, and ultimately utilized through finite, irreversible pathways. At each stage, entropy generation irreversibly degrades usable energy potential, enforcing universal thermodynamic bounds on performance. Consequently, road vehicles, rail systems, marine vessels, and even biologically inspired transport mechanisms are governed by the same underlying principles of energy survival, regardless of their apparent technological diversity.

Observed differences in performance across transportation modes therefore do not arise from fundamentally different physical laws, but from differences in the energy survival factor (Ψ) and the internal conversion competency (C_{int}). Systems such as electric rail benefit from high contact survival and low rolling resistance, yielding larger Ψ values, while internal combustion vehicles are constrained by substantial entropy generation during combustion, resulting in lower survival. Similarly, marine transport performance is limited primarily by hydrodynamic dissipation, whereas road vehicles are dominated by surface contact and auxiliary losses. In each case, the governing law remains unchanged; only the survival structure and conversion capacity differ.

This universality has important scientific and practical implications. It enables direct, physically meaningful comparison across transportation modes using a common thermodynamic framework, rather than mode-specific efficiency metrics that obscure underlying constraints. By demonstrating that all transportation systems are subject to the same survival-based law, the framework provides a unified foundation for cross-modal analysis, technology assessment, and policy evaluation. Ultimately, it establishes that improvements in transportation performance must focus on enhancing energy survival and conversion capacity, rather than seeking fundamentally new laws or relying on isolated efficiency gains.

5. Conclusions

This study establishes a Unified Energy Survival–Absorption–Conversion Law that governs useful energy production across road, freight, rail, and marine transportation systems. By replacing efficiency with a thermodynamically grounded survival framework, the proposed law explains long-observed performance saturation, reconciles laboratory–field discrepancies, and provides a universal basis for system comparison and optimization.

The governing equation

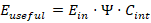
demonstrates that transportation performance is limited by energy survival and conversion capacity, not by peak efficiency.

This framework is experimentally measurable, falsifiable, and broadly applicable, offering a new physical foundation for transportation engineering, sustainability analysis, and energy policy.

References

Banister, D., Anderton, K., Bonilla, D., Givoni, M., & Schwanen, T. (2011). Transportation and the environment. Annual review of environment and resources, 36(1), 247-270.

Blunden, M. (2012). Geopolitics and the northern sea route. International affairs, 88(1), 115-129.

Corbett, J. J. (2004). Marine transportation and energy use. Encyclopedia of energy, 3, 745-758.

Cordon-Lagares, E., & García-Ordaz, F. (2020). Factors affecting the survival of maritime goods transport firms in Spain. Research in Transportation Business & Management, 37, 100520.

Dehalwar, K. S. S. N., & Sharma, S. N. (2024). Exploring the distinctions between quantitative and qualitative research methods. Think India Journal, 27(1), 7-15.

Dehalwar, K., & Sharma, S. N. (2023). Fundamentals of research writing and uses of research methodologies. Edupedia Publications Pvt Ltd.

Dehalwar, K., & Sharma, S. N. (2026). Human Settlements and Social Dynamics: A Planner’s Guide. Cambridge Scholars Publishing.

Fu, B. C. (2022). Unification and coordination of maritime jurisdiction: Providing a judicial guarantee for international trade and marine transport. Frontiers in Marine Science, 9, 848942.

Gilbert, R., & Pearl, A. (2012). Transport revolutions: moving people and freight without oil. Routledge.

Halff, A., Younes, L., & Boersma, T. (2019). The likely implications of the new IMO standards on the shipping industry. Energy policy, 126, 277-286.

Khaskheli, M. B., Zhao, Y., & Lai, Z. (2025). Sustainable Maritime Governance of Digital Technologies for Marine Economic Development and for Managing Challenges in Shipping Risk: Legal Policy and Marine Environmental Management. Sustainability, 17(21), 9526.

Mashrafi, M. (2026). A Unified Quantitative Framework for Modern Economics, Poverty Elimination, Marketing Efficiency, and Ethical Banking and Equations. International Journal of Research, 13(1), 508-542.

Mashrafi, M. (2026). Domain-Dependent Validity of an Inequality Derived from a Classical Absolute Value Identity. International Journal of Research, 13(1), Mashrafi, M. (2026). Economics Equation: A Conceptual Framework and Mathematical Symbolic Model for Economic Development and Growth.

Mashrafi, M. (2026). Universal Life Competency-Ability Framework and Equation: A Conceptual Systems-Biology Model. International Journal of Research, 13(1), 92-109.

Mashrafi, M. (2026). Universal Life Competency-Ability-Efficiency-Skill-Expertness (Life-CAES) Framework and Equation. Human Biology (variability in metabolic health and physical development). International Journal of Research, 13(1),

Mashrafi, M. (2026). Universal Life Energy–Growth Framework and Equation. International Journal of Research, 13(1), 79-91.

Mashrafi, M. Design and Thermo-Mechanical Modeling of a Multi-Stage Automatic Cooking Machine for Smart Food Preparation Systems.

Nowacki, G. (2012). Development and standardization of intelligent transport systems. International Journal on Marine Navigation and Safety of Sea Transportation, 6(3), 403-411.

Odgaard, L. (2023). Russia’s Arctic designs and NATO. In Survival: August-September 2022 (pp. 89-104). Routledge.

Schnurr, R. E., & Walker, T. R. (2019). Marine transportation and energy use. Reference Module in Earth Systems and Environmental Sciences, 10.

Sharma, S. N., & Dehalwar, K. (2025). A systematic literature review of transit-oriented development to assess its role in economic development of city. Transportation in Developing Economies, 11(2), 23.

Sharma, S. N., & Dehalwar, K. (2025). Retracted: Assessing the transit-oriented development and travel behavior of the residents in developing countries: A case of Delhi, India. Journal of Urban Planning and Development, 151(3), 05025018.

Soyer, B., & Tettenborn, A. (Eds.). (2013). Carriage of Goods by Sea, Land and Air: Uni-modal and Multi-modal Transport in the 21st Century. CRC Press.